Przekroje maqki: Sześcian o krawędzi długości 3 przecięto płaszczyzną przechodzącą przez przekątną podstawy i tworzącą z płaszczyzną podstawy kąt α. Oblicz pole otrzymanego przekroju dla a) α=45 stopni b) α=60 stopni Rozwiązanie już jest na forum,ale mam pytanie dlaczego przy 45stopniach przekrojem jest trójkąt,a przy 60 stopniach trapez?

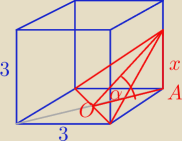
janek191: α =45^o OA = x x = 1,5√2 < 3

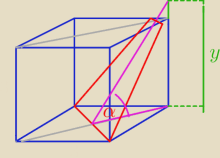
janek191: α = 60^o y = 1,5 √6 > 3

maqki: Hmm wydaje mi się że zrozumiałem. W pewnej książce mam wskazówki żeby sprawdzić jakim wielokątem jest ten przekrój. Mając dana połowę podstawy i wysokość liczymy tg tego kąta, przy którym przekrój z trójkąta '' zmienia się" w trapez równoramienny. I przykładowo dla sześcianu ten kat wynosi około 54°, i przekrojem jest trapez równoramienny. I nie rozumiem dlaczego dla akurat takiego kąta jest to trapez? Są jakieś przedziały tego kąta dla których jest trójkątem lub trapezem?

xyz: z pierwszego rysunku janka jakby ten wierzcholek trojkata podciagnac na sama gore tzn do wierzcholka szescianu to by bylo ze

	3
tg(α) =		≈ ...
	3√2

odczytujesz alfe i wtedy dla kazdego kata wiekszego od alfa bedzie to trapez (rysunek 2) a dla mniejszego rownego alfa bedzie to trojkat (rysunek 1)

xyz: literowka*

	3
tg(α) =
	1   *3√2 2

bo bok szescianu ma dlugosc 3 polowa przekatnej podstawy szescianu (czyli polowa przekatnej kwadratu o boku 3)

	1
to jest		* 3√2
	2

maqki: Dzięki o to mi chodziło. Czyli w sumie dla sześcianu zawsze będzie to kat 54°