| π | ||
x≠− | +kπ | |
| 4 |
| kπ | ||
x = | ||
| 4 |
| 1−cos8x | ||
Rozwiąż równanie | =0 | |
| 1+tgx |
| kπ | π | |||
odpowiedzi: x= | lub x= | +kπ | ||
| 2 | 4 |
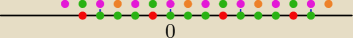Takie rzeczy najlepiej zaznaczyć sobie na osi, najczęściej to na tej zasadzie można określić
całkowite rozwiązanie jak widać:
| π | ||
czerwone −> x ≠− | + kπ | |
| 4 |
| kπ | ||
zielone −> x = | ||
| 4 |
| kπ | ||
fioletowe −> x = | ||
| 2 |
| π | ||
pomarańczowe −> x= | +kπ | |
| 4 |
| kπ | π | |||
wynik z odp pokrywa się z wynikiem x = | odrzucając x ≠− | + kπ  | ||
| 4 | 4 |
| π | π | 3π | ||||
okropeczki idą co | −> | −> | | |||
| 4 | 2 | 4 |
Czyli odpowiedź trzeba wykombinować na taką, jaka jest w zbiorze? Czy można to zapisać
| kπ | π | |||
normalnie jako x= | z jakimś wyłączeniem tego x=− | +kπ ? Jakby to wyglądało? | ||
| 4 | 4 |
| kπ | ||
Tak. Czyli ostatecznie jedyna słuszna odpowiedź to x= | ? | |
| 4 |