Współrzędne wierzchołków trapezu
kk: Punkty
A=(0,4) i D=(3,5) są wierzchołkami trapezu równoramiennego ABCD. Podstawy trapezu
są prostopadłe do prostej
k: x−y−6=0 przechodzącej przez punkt C. Oblicz współrzędne
pozostałych wierzchołków oraz pole trapezu.
Na razie obliczyłem punkt C:
y=−x+b −−> 4=0+b
b=4
−x+8=x−6
x=7
y=7−6=1
C(7,1)
Jak teraz obliczyć punkt B?
4 lut 14:48
Pokojówka Gu :
Skoro obliczles punkt C to latwo obliczyc punkt B
Trapez rownoramienny ma os symetrii
4 lut 15:07
janek191:
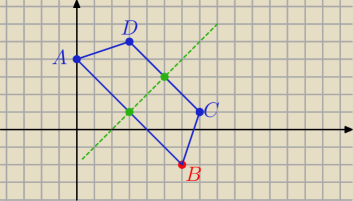
4 lut 15:09
Bogdan:
Można skorzystać z: |BC|2 = |AD|2, B = (xB, yB), B leży na prostej o równaniu: y = ...
4 lut 15:09
kk: ale przecież on będzie miał zupełnie inne położenie w układzie współrzędnych, prawda?
4 lut 15:10
Pokojówka Gu : Prawda . To jest tylko szkic . Patrz tez rysunek janek191
4 lut 15:11
salamandra:
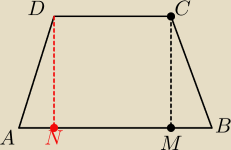
k: x−y−6=0
−y=−x+6
y=x−6
prostopadła do niej:
y=−x+b
A=(0,4)
prosta l (na której leży punkt A i B): y=−x+4
prosta m (na której leży punkt D i C): y=−x+b
D=(3,5)
5=−3+b
b=8
y=−x+8
punkt przecięcia prostej y=x−6 oraz y=−x+4 wyznaczy nam współrzędne punktu M
x−6=−x+4
2x=10
x=5
5−6=y
−1=y
M=(5,−1)
Równanie prostej prostopadłej do AB przechodzącej przez punkt D
y=x+b
D=(3,5)
5=3+b
b=2
y=x+2
Punkt przecięcia prostej DN i AB da nam współrzędne punktu N
y=x+2
y=−x+4
x+2=−x+4
2x=2
x=1
y=3
N=(1,3)
M=(5,−1)
Odległość od N do M to długość podstawy górnej
|NM|
2= (5−1)
2+(−1−3)
2
|NM|
2= 32
|NM|=
√32 = 4
√2
|DC| = 4
√2
Można też zauważyć, że punkt przecięcia prostych y=−x+8 oraz y=x−6 da nam C=(7,1)
I z tego też wynika że od D do C jest 4
√2
| | a+b | |
Wiemy że odcinek od A do M to |
| , dzięki przekształceniom wyliczmy długość "a" (podstawy |
| | 2 | |
dolnej)
A=(0,4)
M=(5,−1)
|AM|
2= 25+25 = 50
|AM|=
√50= 5
√2
10
√2 = a+4
√2
a= 6
√2
Wiemy że długość AB to 6
√2, więc wyliczymy teraz "B"
|AB|
2 = 72
"B" leży na prostej AB, więc B(x, −x+4)
|AB|
2= x
2+(−x+4−4)
2
72= 2x
2 / : 2
36=x
2
x=6 v x= −6
B(6, −2) lub B(−6,10)
Zobacz czy do tego momentu się zgadza?
4 lut 15:15
salamandra: Nie gra mi tylko ten drugi punkt B co mi wyszedł.
4 lut 15:15
Panna Lu: Sprawdz obliczenia
4 lut 15:30
4 lut 15:31
salamandra: Nie widzę u siebie błędu

4 lut 15:46
salamandra: Można to chyba sprawdzić w ten sposób, że BC i AD muszą być równe, więc
B=(6,−2)
C=(7,1)
|BC|2= 1+9 = 10
|BC|= √10
A= (0,4)
D=(3,5)
|AD|2= 9+1= 10
|AD|= √10
II przypadek
B=(−6,10)
|BC|2= 169+81 = 250
|BC| = √250
Nie zgadza się, bo AD zostanie bez zmian.
4 lut 15:50
salamandra: Pole:
| | (a+b)*h | | (6√2+4√2)*h | |
P= |
| = |
| |
| | 2 | | 2 | |
wysokość to dokładnie |MC| lub |ND|
M=(5,−1)
C(7,1)
|MC|
2= 4+4 = 8
|MC| = 2
√2
| | (10√2)*2√2 | | 40 | |
P= |
| = |
| = 20 |
| | 2 | | 2 | |
4 lut 15:53
ite: salamandra B=(6, −2) lub B=(−6,10) obie odpowiedzi są dobre. Istnieją dwa trapezy, które
spełniają warunki zadania
4 lut 16:30
salamandra: Jeśli B(−6,10) to będzie on równoramienny?
4 lut 16:33
ite: oba są równoramienne, zobacz 15:31
4 lut 16:38
ite: To, że trapez jest równoramienny, jest podane w treści zadania. Inaczej byłoby nieskończenie
wiele rozwiązań.
4 lut 16:43
salamandra: Czyli wtedy AB i CD są de facto ramionami (w przypadku B(−6,10))?
4 lut 16:43
ite: W tym przypadku powstaje równoległobok (to też jest trapez równoramienny).
Ale dopiero teraz zwróciłam uwagę, że to daje inną kolejność wierzchołków niż podaną w zadaniu
i mam wątpliwość, czy warunki zadania są spełnione.
4 lut 16:52
ite: Niech wypowie się ekspert, to zawsze jest dobre wyjście

4 lut 16:53
Mila:
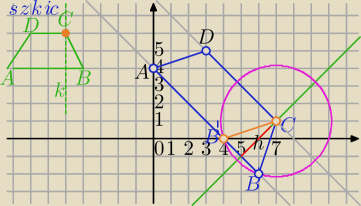
A=(0,4) i D=(3,5) są wierzchołkami trapezu równoramiennego ABCD. Podstawy trapezu
są prostopadłe do prostej k: x−y−6=0 przechodzącej przez punkt C.
k: y=x−6
1) AB⊥k, DC⊥k
2) DC: y=−x+b, b=8 , y=−x+8
Wsp. punktu C
−x+8=x−6
x=7,y=1
C=(7,1)
3) AB: y=−x+4
|AD|=
√32+1=
√10
4) wsp. punktu B :
(x−7)
2+(y−1)
2=10 i y=−x+4⇔
B=(6,−2) lub B'=(4,0)
5) Pole ABCD:
A=(0,4),B=(6,−2) ,C=(7,1), D=(3,5)
|AB|=
√62+62=6
√2
|DC|=4
√2
h− odległość punktu C od prostej AB: x+y−4=0
| | 6√2+4√2 | | 4 | |
PABCD+ |
| * |
| =5*4 |
| | 2 | | √2 | |
P
ABCD=20
| | 4√2+4√2 | | 4 | |
lub PAB'CD= |
| * |
| =... |
| | 2 | | √2 | |
4 lut 18:17
ite: thx

5 lut 15:44
 Skoro obliczles punkt C to latwo obliczyc punkt B
Trapez rownoramienny ma os symetrii
Skoro obliczles punkt C to latwo obliczyc punkt B
Trapez rownoramienny ma os symetrii

 k: x−y−6=0
−y=−x+6
y=x−6
prostopadła do niej:
y=−x+b
A=(0,4)
prosta l (na której leży punkt A i B): y=−x+4
prosta m (na której leży punkt D i C): y=−x+b
D=(3,5)
5=−3+b
b=8
y=−x+8
punkt przecięcia prostej y=x−6 oraz y=−x+4 wyznaczy nam współrzędne punktu M
x−6=−x+4
2x=10
x=5
5−6=y
−1=y
M=(5,−1)
Równanie prostej prostopadłej do AB przechodzącej przez punkt D
y=x+b
D=(3,5)
5=3+b
b=2
y=x+2
Punkt przecięcia prostej DN i AB da nam współrzędne punktu N
y=x+2
y=−x+4
x+2=−x+4
2x=2
x=1
y=3
N=(1,3)
M=(5,−1)
Odległość od N do M to długość podstawy górnej
|NM|2= (5−1)2+(−1−3)2
|NM|2= 32
|NM|= √32 = 4√2
|DC| = 4√2
Można też zauważyć, że punkt przecięcia prostych y=−x+8 oraz y=x−6 da nam C=(7,1)
I z tego też wynika że od D do C jest 4√2
k: x−y−6=0
−y=−x+6
y=x−6
prostopadła do niej:
y=−x+b
A=(0,4)
prosta l (na której leży punkt A i B): y=−x+4
prosta m (na której leży punkt D i C): y=−x+b
D=(3,5)
5=−3+b
b=8
y=−x+8
punkt przecięcia prostej y=x−6 oraz y=−x+4 wyznaczy nam współrzędne punktu M
x−6=−x+4
2x=10
x=5
5−6=y
−1=y
M=(5,−1)
Równanie prostej prostopadłej do AB przechodzącej przez punkt D
y=x+b
D=(3,5)
5=3+b
b=2
y=x+2
Punkt przecięcia prostej DN i AB da nam współrzędne punktu N
y=x+2
y=−x+4
x+2=−x+4
2x=2
x=1
y=3
N=(1,3)
M=(5,−1)
Odległość od N do M to długość podstawy górnej
|NM|2= (5−1)2+(−1−3)2
|NM|2= 32
|NM|= √32 = 4√2
|DC| = 4√2
Można też zauważyć, że punkt przecięcia prostych y=−x+8 oraz y=x−6 da nam C=(7,1)
I z tego też wynika że od D do C jest 4√2


 A=(0,4) i D=(3,5) są wierzchołkami trapezu równoramiennego ABCD. Podstawy trapezu
są prostopadłe do prostej k: x−y−6=0 przechodzącej przez punkt C.
k: y=x−6
1) AB⊥k, DC⊥k
2) DC: y=−x+b, b=8 , y=−x+8
Wsp. punktu C
−x+8=x−6
x=7,y=1
C=(7,1)
3) AB: y=−x+4
|AD|=√32+1=√10
4) wsp. punktu B :
(x−7)2+(y−1)2=10 i y=−x+4⇔
B=(6,−2) lub B'=(4,0)
5) Pole ABCD:
A=(0,4),B=(6,−2) ,C=(7,1), D=(3,5)
|AB|=√62+62=6√2
|DC|=4√2
h− odległość punktu C od prostej AB: x+y−4=0
A=(0,4) i D=(3,5) są wierzchołkami trapezu równoramiennego ABCD. Podstawy trapezu
są prostopadłe do prostej k: x−y−6=0 przechodzącej przez punkt C.
k: y=x−6
1) AB⊥k, DC⊥k
2) DC: y=−x+b, b=8 , y=−x+8
Wsp. punktu C
−x+8=x−6
x=7,y=1
C=(7,1)
3) AB: y=−x+4
|AD|=√32+1=√10
4) wsp. punktu B :
(x−7)2+(y−1)2=10 i y=−x+4⇔
B=(6,−2) lub B'=(4,0)
5) Pole ABCD:
A=(0,4),B=(6,−2) ,C=(7,1), D=(3,5)
|AB|=√62+62=6√2
|DC|=4√2
h− odległość punktu C od prostej AB: x+y−4=0
