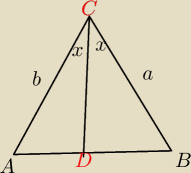
Trójkąt, dowód Deve: W trójkącie ABC w którym AC=b BC=a i kąt ACB równa się 2x, z wierzchołka C poprowadzono dwusieczną kąta która przecięła bok AB w punkcie D, wykaż że CD=2abcosx/a+b

deve:

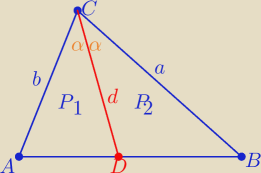
a@b: 2P₁= bdsinα , 2P₂=d*a*sinα 2P(ABC) = ab*sin(2α) , sin2α= 2sinα*cosα to: dsinα(a+b)=2ab sinα*cosα

	2abcosα
d=|CD|=
	a+b

===============