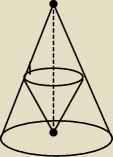
 Witam, to znowu ja i kolejny problem matematyczny
tym razem próbuję narysować stożek. W stożek Sw został wpisany drugi stożek Sw. Jaką częścią
objętości stożka Sz jest największa objętość stożka Sw?
Witam, to znowu ja i kolejny problem matematyczny
tym razem próbuję narysować stożek. W stożek Sw został wpisany drugi stożek Sw. Jaką częścią
objętości stożka Sz jest największa objętość stożka Sw?
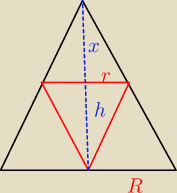 x+ h = H
z tw. Talesa:
x+ h = H
z tw. Talesa:
| x | r | ||
= | |||
| x+h | R |
| 1 | ||
Vm = | πr2*h | |
| 3 |
| 1 | ||
Vd = | πR2*H | |
| 3 |
| Vm | r2*h | r | h | x2*h | x2(H−x) | ||||||
= | = ( | )2* | = | = | |||||||
| Vd | R2*H | R | H | H3 | H3 |
| x2(H−x) | ||
f(x) = | szukasz maksimum tejże funkcji | |
| H3 |
 !
!