kolejna zagwostka jakzdacmature: Witam, Napisz równania okręgów stycznych jednocześnie do osi Ox i do prostej o równaniu y= 4/3 x, które przechodzą przez punkt P=(6,2) Miłego wieczoru!

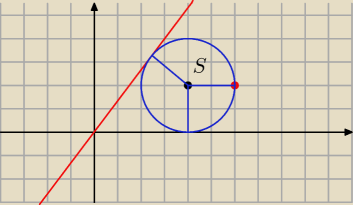
Saizou : Czyli szukasz takiego punktu S, który jest równoodległy od osi OX oraz prostej i punktu P S leży na dwusiecznej kąta, jaki tworzy oś OX i prosta (zgodnie z definicją dwusiecznej) i dalej sam

jc: Znajdź na dwusiecznej, czyli na prostej y=x/2, punkty równo oddalone od osi Ox i puntu P. To będą środki szukanych okręgów.

jc: Punkty równo odległe od osi i od punktu P leżą na paraboli 4y=x² −12x +40. Przecięcie: 2x = x² − 12x +40, x² −14x+40=0, x=4 lub x=10. Środki: (4,2), (10,5). Promienie oczywiście 2 i 5.

jakzdacmature: Przyjmuję, że S=(a, b). Obliczyłam odległość punktu S od prostej 4x−3y=0 i prostej y=0 (każda z tych odleglosci to promień okręgu) . Wyszła mi zależność a=2b lub a= − 0,5b. Dodatkowo |SP| = r. Po zabawie z równaniami wyszło mi, że S(4,2) lub S(10,5). Dobrze myślę?

jakzdacmature: Ah, nie odświeżyłam.. Super, dziękuję za pomoc