twierdzenie sinusów i cosinusów
salamandra: Obwód trójkąta równobocznego jest równy 3a. Punkty A1, B1, C1 należą odpowednio do boków AB,
BC, CA, przy czym |AA1|=|BB1|=|CC1|=x. Oblicz dla jakiej wartości pole trójkąta A1B1C1 jest
najmniejsze.
Gdy pojawiają się same literki, brak mi kompletnie pomysłu co wyznaczyć, jak wyznaczyć, z czego
wyznaczyć.
Mam jedynie rysunek.
2 lut 21:30
salamandra:
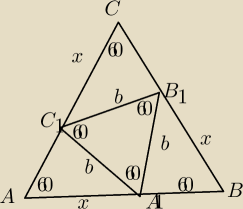
2 lut 21:31
Saizou :
Podpowiedź
Uzależnij b od zmiennych a oraz x (zmienna a może zostać w wyniku)
np. |A1B|=a−x
2 lut 21:34
salamandra: b2= x2+(a−x)2−2*x*(a−x)*cos60?
2 lut 21:39
Saizou : Chociaż łatwiej, od dużego trójkąta, odjąć pola tych "narożnych"
2 lut 21:40
Mila:
Licz pola naroży i odejmij po pola ΔABC

2 lut 21:41
janek191:
| | a2 √3 | |
P(x) = |
| − 3*0,5*x*(a −x)*sin 60o = |
| | 4 | |
2 lut 21:42
Leszek: PΔ(A
1B B
1 ) = (1/2)x(a−x) sin 60°
| | a2√3 | |
P(x) = |
| − (3/2) x( a−x) √3/2 = ....... |
| | 4 | |
2 lut 21:44
salamandra: | | 1 | |
PAA1C1 = x*(a−x)*sin60* |
| |
| | 2 | |
Pozostałe dwa przystające, więc
| | √3 | | √3ax−x2*√3 | | √3(ax−x2) | |
Pole narożnych: 3*(ax−x2)* |
| = 3*( |
| ) = 3*( |
| ) = |
| | 4 | | 4 | | 4 | |
Dobrze do tego momentu?
2 lut 21:48
Saizou :
To ja pociągnę moją pierwszą wersję z liczeniem b
z tw. cosinusów
b
2=x
2+(a−x)
2−2x(a−x)cos60
b
2=x
2+a
2−2ax+x
2−ax+x
2
b
2=3x
2−3ax+a
2
| | b2√3 | | √3 | |
P=PA1B1C1= |
| = |
| (3x2−3ax+a2) |
| | 2 | | 2 | |
Szukamy najmniejszej wartości funkcji w nawiasie powyżej
Chyba nawet mniej liczenia
2 lut 21:54
salamandra: No już właśnie zrobiłem tą metodą, ale jestem ciekaw tej drugiej też, czy wyjdzie.
2 lut 21:55
2 lut 21:55
salamandra: Czyli po prostu, jak to pole ma zależeć od x, to muszę kombinować tak, żeby w tym wzorze na
pole znalazł się ten x tak?
2 lut 22:00
Saizou :
No tak, inaczej to nie ma sensu

2 lut 22:02
salamandra: Nie lubię takich zadań... mam nadzieję, że na maturze się nie zdarzają takie stricte
"literkowe"
2 lut 22:06
Saizou : ćwicz takie zadania, jak je opanujesz liczby nie będą przeszkoda

2 lut 22:07
salamandra: Zbiory Kiełbasy zamówione − od wtorku zaczynam maraton

2 lut 22:10
Saizou : A obecnie widzę, że Podkowa

2 lut 22:42
salamandra: Taak, z tej książki na lekcji korzystamy

− muszę przyznać, że generator testów z tej książki
ma bardzo trudne zadania (w porównaniu do zadań w książce, na sprawdzianie większość jest
zaskoczona poziomem

)
2 lut 22:44
Saizou :
Ja lubię Nową Erę jeśli chodzi o zbiór zadań, jakoś Kiełbasa mi nie podpasował jeśli chodzi
o zadania i szatę graficzną.
2 lut 22:47
Mila:
Saizou nie wiesz co się dzieje z małolatem?
2 lut 22:55
Saizou :
Nie mam pojęcia, ale ostatnio mi się jego zachowanie nie podoba.
2 lut 22:59
Mila:
Dawno go tu nie było, może chory, albo wyjechał do Niemiec do córki

Szkoda, że nic do nas nie pisze.
2 lut 23:03
salamandra: @Saizou, no Patryk mi go wczoraj polecił, najwyżej będę żałował, ale czasu zbyt dużo nie ma,
więc dobry będzie i on

zadziwiające jest, jak każdy, co roku, budzi się 3 miesiące przed
maturą

2 lut 23:15
Saizou :
@salamandra ten zbiór pod względem zadań jest okej, tylko mi nie przypadł do gustu.
Jak ja jeszcze uczyłem się do matury, to głownie robiłem zadania z forum tutaj
(no i to co na lekcje)
3 lut 00:03






 − muszę przyznać, że generator testów z tej książki
ma bardzo trudne zadania (w porównaniu do zadań w książce, na sprawdzianie większość jest
zaskoczona poziomem
− muszę przyznać, że generator testów z tej książki
ma bardzo trudne zadania (w porównaniu do zadań w książce, na sprawdzianie większość jest
zaskoczona poziomem  )
)
 Szkoda, że nic do nas nie pisze.
Szkoda, że nic do nas nie pisze.
 zadziwiające jest, jak każdy, co roku, budzi się 3 miesiące przed
maturą
zadziwiające jest, jak każdy, co roku, budzi się 3 miesiące przed
maturą 