Szkic wykresu funkcji i ekstrema lokalne Marcin: Naszkicuj wykres funkcji f: R −> R, jeśli wiadomo, że f'(1) = 0, f'(x) < 0 dla x > 1 oraz f''(x) < 0 dla x ∊ R a) f posiada/nie posiada ekstremum lokalnego w punkcie x0 = 1, bo... b) f na przedziale (−∞, 1) jest ..., bo ... Z tego co rozumiem, to podane w zadaniu informacje mówią: − f'(1) = 0 − w zerze funkcja ma ekstremum lokalne − f'(x) < 0 dla x > 1 − funkcja jest malejąca dla x ∊ (1, ∞) − f''(x) < 0 dla x ∊ R − funkcja nie ma punktów przegięcia Nie za bardzo wiem jak narysować wykres funkcji która ma ekstremum lokalne i jednocześnie nie ma punktu przegięcia. W podpunkcie a) odpowiedziałbym, że funkcja posiada ekstremum lokalne w punkcie x0 = 1, bo f'(1) = 0 W b) zupełnie nie mam pomysłu Z góry dziękuję za wszelkie podpowiedzi

albi: Może nie patrz na f"(x) jako na pochodną drugiego rzędu funkcji f(x) a jak na funkcję pochodną f'(x)

ABC: pierwsza linijka pod słowami "Z tego co rozumiem..." − źle rozumujesz

Marcin: Więc gdy spojrzę na f''(x) jako pochodną pochodnej, to mogę wywnioskować że f'(x) jest malejąca dla x ∊ R, ale co dalej? Wciąż nie wiem, czy f'(x) dla x ∊ (−∞, 1) jest dodatnia, czy ujemna.

ABC: jak nie wiesz jak wiesz z tych danych

Marcin: Więc... f'(x) będzie dodatnia dla x ∊ (−∞, 1), skoro jest malejąca dla x ∊ R, f'(1) = 0 oraz? f'(x) < 0 dla x > 1. Gdyby nie była dodatnia dla x ∊ (−∞, 1), to na logikę, musiałaby być w tym przedziale rosnąca

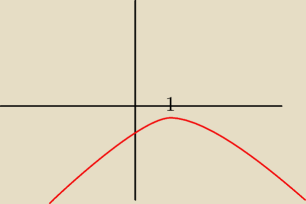
Marcin: Dobra, chyba ogarnąłem: funkcja posiada ekstremum lokalne w x₀ = 1 a na przedziale (−∞, 1) jest malejąca. Czy to jest dobre rozwiązanie?

albi: Chyba chodziło Ci o rosnącą na przedziale (−∞;1), poza tym wydaje się okej.

Marcin: Rosnącą, racja. Tak czy siak, dzięki za pomoc

ds: f(x)=−(1/x−2)