Twierdzenie sinusów i cosinusów salamandra: Podpowiedziałby ktoś z 4.38? https://imgur.com/a/LacYtCh

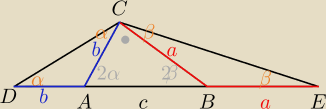
Saizou : Podpowiedź Tw. sinusów w ΔCDE

a+b+c
	=2R
sin(90+α+β

salamandra: A skąd wiadomo ze kąt np. CAB jest dwa razy większy niż CDA?

Saizou : Z trójkątów równoramiennych ∠CAD=180−2α

	180−180+2α
∠ADC=∠ACD=		=α
	2

salamandra: Czyli sin(90+α+β) = cos45, bo 2α+2β=90, wiec α+β=45

	a+b+c
Wiec		= 2R
	√22

2R=2√2p R=p√2 Dzięki Saizou

Mila: Możesz skorzystać z tw. : Kąt zewnętrzny trójkąta jest równy sumie kątów wewnętrznych do niego nieprzyległych. Stąd: ∡CAB=α+α=2α ∡CBA=2β