Zbadaj ekstrema funkcji maMaT : 1. Zbadaj ekstrema funkcji: y=|x²−3x+2| Bardzo proszę o pomoc w rozwiązaniu tego zadania. Kompletnie nie wiem jak się za nie zabrać. Wcześniej nie spotkałem się, z takim rodzajem przykładu.

Jerzy: Prosto: f_min = 0 ,a f_max = f(x_w}

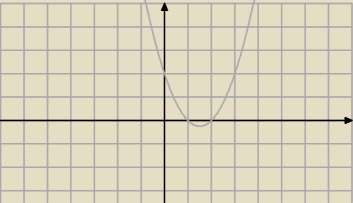
janek191: Odbij symetrycznie względem osi OX część wykresu znajdującego się pod osią. Minima lokalne: x = 1, x = 2 x

janek191: Oraz maksimum lokalne dla x = 1,5

Jerzy: Jasiu, x = 1 lub x = 2 , to nie są minima lokalne

Des: Funkcja nie jest różniczkowalna dla x=1 i x=2, więc nie można mówić o ekstremach w tych punktach

maMaT : Mógłbym prosić o rozpisanie tego? Potrafię zbadać ekstrema w funkcjach, ale w tej tj. z wartością bezwzględną, nie wiem jak postępować.

Jerzy: @Des, błądzisz,tam są minima lokalne.

Blee: Des ... to że funkcja nie jest różniczkowalna w danym punkcie nie oznacza, że nie może być w tym miejscu ekstremum lokalnego (bądź globalnego) Przykład: f(x) = |x| <−−− w x=0 masz MINIMUM GLOBALNE

Jerzy: mamat, narysuj wykres,to zobaczysz ekstrema lokalne.

Des: Minimum globalne tak, ale chyba nie można mówić o lokalnych w tym przypadku?

Blee: dlaczego A jaka jest definicja ekstremum lokalnego

Jerzy: Te dwa minima lokalne są jednocześnienie minimum globalnym.

Blee: definicja minimum/maksimum lokalnego NIC NIE MÓWI o tym, że funkcja ma być różniczkowalna ... baaa ... nawet nie musi o tym, że funkcja ma być ciągła

janek191: Minima lokalne są w punktach x₁= 1 , x₂= 2

Blee: Des ... prawdą jest, że warunkiem WYSTARCZAJĄCYM aby dla x = x₀ było ekstremum lokalne jest to aby f'(x₀) = 0 ∧ f''(x₀) ≠ 0, ale to NIE JEST warunek konieczny

Des: To chyba mylnie zinterpretowałem te ekstrema... myślałem, że o lokalnych jest mowa w punktach w przypadku, gdy funkcja w tych otoczeniach jest różniczkowalna czyli są one ściśle związane z pochodną... a jednak nie do końca

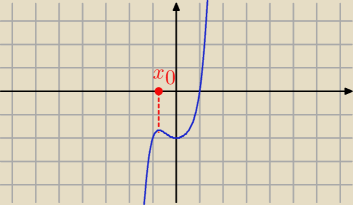
janek191: Def. Funkcja f określona w otoczeniu punktu x_o, ma w punkcie x_o maksimum lokalne, jeżeli istnieje taki przedział ( x₀ − δ; x₀ +δ), że f(x) ≤ f(x₀) , dla x ∊ (x₀ −δ, x₀ +δ).

maMaT : Jest to jedno z zadań na egzamin. Tak jak nie mam problemu z innymi zadaniami z ekstremum, tak z tym nie wiem jak postąpić. Muszę rozpisać ten przykład, aby został zaliczony, nie mogę narysować wykresu.

Jerzy: Możesz.

Blee: ale nie musisz ... szkic wykresu pochodnej (określenie monotoniczności) + pokazanie, że funkcja jest ciągła w D_f = R będzie wystarczające, aby wysnuć wniosek, że w x=1 i x=2 masz minima lokalne

maMaT : a mimo wszystko mogę Was prosić o rozpisanie tego przykładu? taki sposób jest dla mnie bardziej zrozumiały. Czy mogę wyjść z wartości bezwględnej, rozpatrując dwa przypadki, tj. x dla x≥0 i −x dla x<0?