funkcja logarytmiczna Agula: Jak narysować wykres funkcji: g(x)=(¹₂)^If(x)I gdzie f(x)=log₂x

Zielona Gałązka: W wykładniku podstaw wzór f(x) i rozpatrz 2 przypadki wartości bezwzględnej I f(x) I Otrzymasz takie fajne zapisy, gdzie Ci się troszkę poskraca. Jest taki wzór: a do potęgi o wykładniku logarytm przy podstawie a, z liczby X, równa się X

tim: Gałązka − dla x = 0,5, się skróci, ale dla np. x = 3 (jak?)

Agula: moglbys mi to jednak jakos rozpisac te dwa przypadki, bo tak nie bardzo jarze o co chodzi

Agula: prosze to ma byc dla x<1 i dla x>1 czy jak

Agula: tim

tim: UWAGA! Aby logarytm zachodził x > 0. Zatem: Dla x > 1 mamy: 0,5^log₂x Dla 0 < x ≤ 1 mamy: 0,5^{−1 * log₂x} = 2^log₂x = x

tim: Tzn dziedziną funkcji jest x > 0, gdyż log₂x, gdzie x > 0.

tim:

	1
0,5log2x =
	x

tim: Więc rysuesz funkcję y = x, od 0 (otwarte) do 1 i funkcję 1/x od 1 do +∞. { 1/x x ∊ (1, +∞) g(x) = { x x ∊ (0, 1>

Agula: dziekuje bardzo

ds: oblicz x gdy : log_0,5(log₂x)=1

Paweł 19 : Może mi ktoś wyjaśnić dlaczego rozbijamy tą wartość bezwględną na x>1 i 0<x≤1 ? I dlaczego jak jest 0<x≤1 to mamy 0.5* ⁽−1)*log₂ x Nie wiem dlacyego tak jest, proszę o pomoc

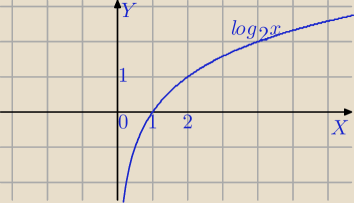
Mila: D: x>0 Dla x∊(0,1) funkcja f(x) =log₂x przyjmuje wartości ujemne Dla x≥1 funkcja f(x) =log₂x przyjmuje wartości nieujemne 1) |log₂(x)|=−log₂(x) dla x∊(0,1) 2) |log₂(x)|=log₂(x) dla x≥1 stąd: 1) dla x∊(0,1)

	1		1
(		)|log2(x)|=(		)−log2(x)=2log2(x)=x
	2		2

2)dla x≥1

	1		1
(		)|log2(x)|=(		)log2(x)=(2−1)log2(x)=2−log2(x)=
	2		2

	1
=2log2(x−1)=
	x

Potrafisz teraz narysować wykres?