Ograniczoność i różniczkowalność funkcji Marcin: Niech f(x) = |x − 1| dla x ∊ <−2, 2>. Wówczas funkcja f a) jest/nie jest ograniczona w <−2, 2>, bo... b) jest/nie jest całkowalna w przedziale <−2, 2>, bo... W a) napisałbym, że funkcja nie jest ograniczona w <−2, 2>, ponieważ f(−2) = 3, co wychodzi poza przedział. W b) funkcja jest całkowalna w przedziale <2, 2> ponieważ jest ciągła Takie uzasadnienia są dobre? Nie jestem pewien czy dobrze rozumiem podpunkt a), na moją logikę funkcja byłaby ograniczona w przedziale <−2, 2> gdyby jej wartości dla arugmentów z przedziału <−2, 2> zawierały się w przedziale <−2, 2>, więc skoro f(−2) = 3, to funkcja nie jest ograniczona w danym przedziale

Blee: a) każda funkcja ciągła na przedziale domkniętym BĘDZIE ograniczona (z góry i dołu) b) nie jest całkowalna, ponieważ nie jest całkowalna w punkcie x=1 (dowodzisz to próbując policzyć pochodną w tymże punkcie z definicji)

Blee: (a) jako przykład −−− popatrz na funkcję f(x) = lnx w D_f = R₊ funkcja ta z oczywistych względów NIE JEST ograniczona, ale jakikolwiek (domknięty) zbiór dla 'x' weźmiemy, to dla tegoż przedziału ta funkcja będzie ograniczona

Marcin: Więc w b) liczę pochodną w x=1 w następujący sposób: lim Δx −> 0 ^{f(1+Δx) − f(1)}_Δx = lim Δx −> 0 ^{|1+Δx−1| − |1−1|}_Δx = lim Δx −> 0 ^Δx_Δx = ⁰₀, czyli symbol nieoznaczony, więc pochodna nie istnieje a co za tym idzie funkcja nie jest całkowalna?

Blee: NIE

	|Δx|
masz limΔx −> 0		= (*)
	Δx

więc liczymy granice jednostronne:

	−Δx
limΔx −> 0−		= −1
	Δx

	Δx
limΔx −> 0+		= 1
	Δx

związku z tym (*) <−−− nie istnieje (granice jednostronne nie są sobie równe)

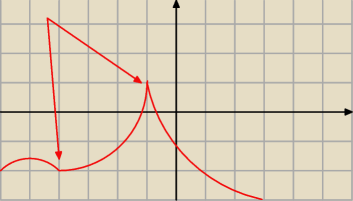
Blee: ogólna 'wskazówka' −−− funkcja nie będzie całkowalna w jakimś punkcie, jeżeli (pomijając kwestię nieciągłości samej funkcji) w tym punkcie ma miejsce 'mocny pik' (patrz wykres f(x) = |x−1| <−−− w x=1 masz tenże 'pik' ; albo zobacz wykres który narysowałem − w zaznaczonych punktach funkcja ta NIE JEST całkowalna

Marcin: Skąd bierze się wzór lim Δx −> 0 ^|Δx|_Δx ? Wszędzie gdzie szukałem widziałem wzór lim Δx −> 0 ^{f(x0 + Δx) − f(x0)}_Δx, według którego gdy liczę granicę obustronną to i z lewej i z prawej wychodzi mi 1

Marcin: Nie ważne, przeoczyłem z jakiegoś powodu że u góry ułamka dalej zostaje moduł po tym gdy skrócą się jedynki. Teraz wszystko łączy się w całość.

Blee: zamiast Δx będę pisał h (leniem jestem)

	f(1 + h) − f(1)		|1 − 1 + h| − | 1 − 1 |
limh−>0		=		=
	h		h

	|0 + h|		|h|
= lim		= lim
	h		h