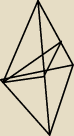
ostrosłup hubik: Jak na rysunku jest ostrosłup prawidłowy, z podstawą trójkąta równobocznego o bokach równych 6. Na jednej ze ścian zaznaczony jest trapez równoramienny, o krótszej podstawie, równej 4. Płaszczyzna trójkąta, wychodzącego z podstawy jest prostopadła do płaszczyzny ściany ostrosłupa. Wyliczyłem wysokość trójkąta wychodzącego z podstawy, wysokość podstawy i nawet odległość między kątem, z którego wychodzi trójkąt prostopadły do ściany, a podstawą wysokości trapezu, ale wszystkie b ( długość boku trójkąta prostopadłego ) mi się zerują i nie mogę wyliczyć wysokości trapezu, która jak mi się wydaje jest potrzebna do wyliczenia wysokości z podobieństwa trójkątów. Pomocy XD

ite: Płaszczyzna trójkąta, wychodzącego z podstawy, jest prostopadła do płaszczyzny ściany ostrosłupa. OK, ale skąd wiadomo, że trzecim wierzchołkiem takiego trójkąta jest wierzchołek podstawy ostrosłupa? Nie podajesz treści zadania.

hubik: Treść jest taka: Podstawą ostrosłupa prawidłowego ABCS jest trójkąt równoboczny ABC o boku długości 6. Na krawędziach bocznych BS i CS wybrano punkty, odpowiednio D i E, takie że |BD| = |CE| oraz |DE| = 4. Płaszczyzna ADE jest prostopadła do płaszczyzny ściany bocznej BCS ostrosłupa. Oblicz objętość ostrosłupa

www: https://zadania.info/d1535/1199830