W sześcianie ABCDA'B'C'D' punkt P jest środkiem przekątnej ściany bocznej BCC'B
Marek: W sześcianie ABCDA'B'C'D' punkt P jest środkiem przekątnej ściany bocznej BCC'B' i jego
odległość od przekątnej sześcianu BD' jest równa √2.
Oblicz objętość tego sześcianu.
31 sty 22:05
Szkolniak: Objętość wyszła mi 8, masz odpowiedź do tego zadania?
31 sty 22:33
a@b:
V=24√3
31 sty 22:35
Szkolniak: 
jaki wyszedł Ci bok sześcianu
a@b?
31 sty 22:40
a@b:
a=2√3
31 sty 22:41
a@b:
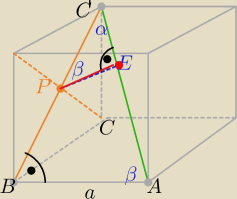
Z podobieństwa trójkątów prostokątnych ( kkk)
.................
.................
a=2
√3
31 sty 22:46
Szkolniak: Rzeczywiście, w jednym trójkącie nie wychodzi mi równość z Pitagorasa, więc musiałem gdzieś
namieszać

31 sty 22:47
a@b:

31 sty 22:48
Blee:
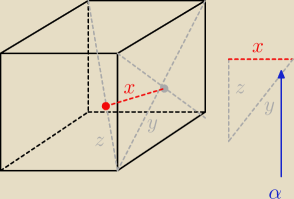
x =
√2
| | √2 | |
y = |
| a (połowa przekątnej ściany boczne ; gdzie a −−− długość boku) |
| | 2 | |
α = 45
o
| | x | | √2 | | 2 | | √2 | |
cosα = |
| = |
| = |
| = |
| −> a = 2√2 |
| | y | | a√2/2 | | a | | 2 | |
V = a
3 = 16
√2 [j
3]
PS. Zastanów się skąd wiem, że α = 45
o
31 sty 23:00
Blee:
oczywiście namieszałem z długościami

31 sty 23:01
a@b:
?
Ja się nie zgadzam

31 sty 23:02
a@b:
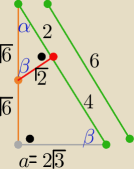
31 sty 23:13
a@b:
Hej
Blee żyjesz?

31 sty 23:17
a@b:
Dodam,że
dla krawędzi sześcianu o długości "a"
odległość środka ściany od przekątnej sześcianu jest równa
d=a
√6 /6
========
w tym zadaniu d=
√2 ⇒ a= 2
√3
i wszystko jasne

Szkoda ,że nasz ....
Blee nie daje znaku .....( że pokićkał rozwiązanie)

1 lut 01:07
 jaki wyszedł Ci bok sześcianu a@b?
jaki wyszedł Ci bok sześcianu a@b?
 Z podobieństwa trójkątów prostokątnych ( kkk)
.................
.................
a=2√3
Z podobieństwa trójkątów prostokątnych ( kkk)
.................
.................
a=2√3


 x = √2
x = √2




 Szkoda ,że nasz .... Blee nie daje znaku .....( że pokićkał rozwiązanie)
Szkoda ,że nasz .... Blee nie daje znaku .....( że pokićkał rozwiązanie) 