Funkcja wymierna z parametrem BoosterXS: Dla jakich wartości parametru m (m ∊ R) zbiór rozwiązań nierówności x²+(m−1)x+m² ≤ 0

	x−1
zawiera się w zbiorze rozwiązań nierówności		< 0?
	x+1

	x−1
Rozwiązuję najpierw		< 0
	x+1

Odp. x∊(−1;1) Założenia do f. kwadratowej: Δ ≥ 0 f(1) > 0 f(−1) > 0 −1 < p < 1

	1
Po rozwiązaniu tych warunków otrzymuję przedział m∊<−1;		>, a w odpowiedziach jest m ∊
	3

(−oo, −1) ∪ (0,+oo). Podpowie ktoś, gdzie popełniłem błąd w założeniach?

BoosterXS:

	1
Pomyłka, otrzymuję zbiór ostatecznie m∊(0;		>
	3

Mila: Musiałeś, źle zobaczyć odpowiedź.

ite: Milu Czy nie należy jeszcze wziąć pod uwagę, że jeśli dla nierówności kwadratowej zachodzi Δ<0, to zbiór jej rozwiązań jest pusty? A zbiór pusty zawiera sie w każdym innym zbiorze.

Pat: Czy mógłby mi ktoś wytłumaczyć na chłopski rozum, dlaczego w założeniach jest f(1) > 0 i f(−1)>0, Domyślam się, że gdyby 1 i −1 byłyby pierwiastkami funkcji f(x) to ich wartość funkcji w tych punktach byłaby 0. Ale, dlaczego nie może być np. f(1)<0

Blee: Pat zauważ, że: 1) wiemy, że 'parabola ma ramiona skierowane do góry'

	x−1
2) nierówność		< 0 jest spełniona dla przedziału x∊ (−1;1)
	x+1

3) w takim razie parabola z (1) nie może przyjmować wartości niedodatnich (ujemne bądź =0) poza obszarem z (2) 4) w związku z tym musi zachodzić f(−1) > 0 oraz f(1) > 0 (oraz x_wierzchołka ∊ (−1;1)) oraz Δ ≥ 0 <−−− mamy wtedy pewność, że parabola przyjmuje wartości niedodatnie tylko (gdzieś tam) w przedziale (−1;1)

Pat: Okej dziękuję, wyobraziłem sobie wszystko po kolei i wydaje mi się to już zrozumiałe

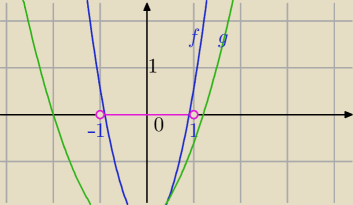
Mila: 1) Niebieski typ wykresu dla paraboli, wtedy f(x)≤0 dla x∊<x₁,x₂>⊂(−1,1) Stąd: f(−1)>0 i f(1)>0 x_w∊(−1,1) 2) Dla g(x) z wykresu zielonego zbiór rozwiązań nierówności g(x)≤0 nie zawiera się w zbiorze (−1,1).