wzory hubik: Przygotowuję się do matury rozszerzonej z matematyki i natrafiłem na pewien problem związany ze wzorami na pole trójkąta Mianowicie, istnieją dwa wzory:

	1
P =		*a*b*sinα
	2

Gdzie alfa to kąt pomiędzy dwoma bokami, i

	1
P =		*a*h
	2

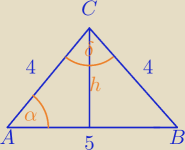
gdzie h jest wysokością, opuszczoną na bok a Weźmy sytuację w której mamy trójkąt równoramienny, z kątem pomiędzy równymi bokami wynoszącym 60 stopni a boki mają długość: 4, 4 i 5 Według pierwszego wzoru:

	1		√3
P =		*16*
	2		2

P = 4√3 Według drugiego wzoru Po opuszczeniu h na bok o długości 5, mamy trójkąt prostokątny z przyprostokątnymi 2,5 i h, plus przeciwprostokątną o długości 4 Z pitagorasa

	25
h2 = 16−
	4

	√39
h =
	2

A z funkcji trygonometrycznych:

	2,5
tg30 =
	h

	2,5
h=
	tg30

	3
h= 2,5*
	√3

	7,5*√3
h=
	3

	5√3
h=
	2

i tutaj już widzimy różnicę w wynikach, pole trójkąta wychodzi oczywiście też inne. Najprawdopodobniej robię błąd rachunkowy którego nie widzę, więc bardzo proszę o pomoc

salamandra: 5²= 16+16−32*cos60

	1
25= 0*
	2

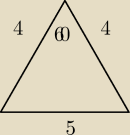
25≠0 Nie ma takiego trójkąta, który miałby boki 4,4,5 i kąt zawarty między ramionami miałby 60 stopni.

salamandra: 25=32−16 25≠16 poprawka, najpierw trzeba wymnożyć cos60*32

a7: trójkąt równoramienny który ma kąt 60 między równymi ramionami to trójkąt równoboczny gdyż pozostałe dwa kąty przy podstawie bedą rowne (180−60):2, więc Twój błąd to źle dobrany trójkąt stąd dalszy galimatias− a raczej niespójność/niezgodność w obliczeniach

Mila:

	5
1)h2+		)2=42
	2

	25
h2=16−
	4

	3		39
h2=9		=
	4		4

	√39
h=
	2

	1		√39		5√39
PΔ=		*5*		=
	2		2		4

2)

	h		√39   2		√39
sinα=		=		=
	4		4		8

	1		√39		5√39
PΔ=		*5*4*		=
	2		8		4

3) Z tw. cosinusów: 25=4²+4²−2*4*4*cosδ −7=−32cosδ

	7
cosδ=
	32

	7		49		975		25*39
sin2δ=1−(		)2=1−		=		=
	32		1024		1024		1024

	5√39
sinδ=
	32

	1		5√39		5√39
PΔ=		*4*4*		=
	2		32		4

Jak nie staniesz to plecy z tyłu