wartość bezwzględna
salamandra: Skoro √x2 = |x| to dlaczego kiedy mam do policzenia odległość i wynosi ona √(−x2+4)2, to
po opuszczeniu pierwiastka zostaje −x2+4, bez wartości bezwzględnej− wynika to z tego, że
odległość nie może być ujemna i dlatego od razu pozbyto się wartości bezwzględnej, która
powinna tam być?
31 sty 17:20
Mila:
√(−x2+4)2=|−x2+4|
31 sty 17:23
Mila:
√(−x2+4)2=−x2+4 tylko dla x∊<−2,2>
31 sty 17:26
salamandra: No właśnie ale już chyba wiem, aby się upewnić napiszę całe zadanie:
https://imgur.com/a/mFzF8jB
Chodzi o to, że bok AD to 2x, więc nie może on być ujemny, stąd bierzemy pod uwagę x∊(0;2), tam
funkcja jest dodatnia, więc wartość bezwzględną opuszczamy bez zmiany znaku?
31 sty 17:29
Mila:
Zgadza się, podano założenie dla x.
|−x2+4| =−x2+4 dla x∊<−2,2> i dodatkowo x>0⇔x∊(0,2)
31 sty 17:49
salamandra: Nie rozumiem dlaczego zawężamy się tylko do przedziału (0;2), dlaczego nie bierzemy pod uwagę
całej dziedziny, czyli (−2, 2).
Mam teraz do tego zadanie już bez rozwiązania:
Oblicz największą wartość pola prostokąta, którego dwa wierzchołki leżą na paraboli o równaniu
y=x2, a dwa pozostałe na cięciwie paraboli wyznaczonej przez prostą o równaniu y=3
A=(−x, 3)
B=(x,3)
C(x,x2)
D=(−x, x2)
|AB|= √4x2 = 2x2 dla x>0
|AD|= √(x2−3)2 = x2−3 dla x (−∞; −√3) U (√3; ∞)
Nie wiem jakie mam brać warunki dla x, i tak jak napisałem wcześniej− dlaczego skupiamy się
tylko na tym wąskim przedziale (0;2) i jak to przełożyć na to zadanie, które teraz robię?
31 sty 17:50
Mila:
Ze względu na symetrię.
Zauważ, że :
Pole po prawej : P1(x)=x*(−x2+4)=P2 po lewej.
Dla uproszczenia rachunków:
P(x)=2x*(−x2+4)
31 sty 18:02
salamandra: Rozumiem, ale nadal nie wiem jak to się ma do tego założenia x>0, a co jakbym chciał to zrobić
w całym przedziale?
31 sty 18:28
salamandra: Bo autor liczy jednak pole całego prostokąta, a nie tego "po prawej" i mnoży *2, ale robi to z
założeniem x∊(0;2)
31 sty 18:31
salamandra: I licząc załóżmy to pole po lewej:
to D(−x,0)
więc odległość odcinka od początku układu współrzędnych do D to √(−x)2− i tutaj też−
dlaczego nie jest |x|, tylko x?
31 sty 18:35
Mila:
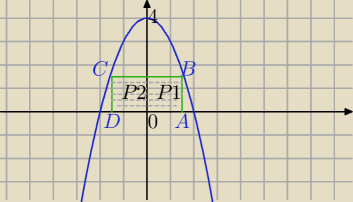
y=−x
2+4
B=(x,4−x
2), C=(−x, −x
2+4)
A=(x,0), x>0, bo A leży po prawej stronie OY
D=(−x,0)
|AD|=|2x|=2x, |AD|=|BC|
|AB|=
√(−x2+4)2=−x
2+4 dla x>0 i x<2 bo punkt A nie może leżeć poza wykresem
P
▭=|AD|*|AB|=2x*(−x
2+4)
=======================
Może obliczyć tyko pole prostokąta po prawej i pomnożyc przez 2 (symetria)
albo policzyć P1 i pole po lewej wtedy:
P(x)=P1(x)+P
2(x) ale po co ?
31 sty 18:51
salamandra: Czyli idąc "od tyłu", gdybym napisał D=(x,0) x<0, to wtedy A(−x, 0) (ze względu na symetrię i
wyszłoby to samo)− o to chodzi mniej więcej?
31 sty 18:55
Mila:
Zawsze musisz pamiętać o znaku liczby opuszczając znak wartości bezwzglednej.
31 sty 19:10
salamandra:
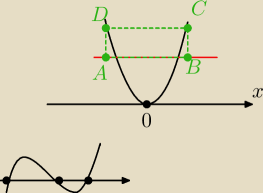
Dlatego, skoro założę x<0 i D(x,0), to A będzie miało x "przeciwny", czyli −x?
Ok, idąc do tego ćwiczenia:
Oblicz największą wartość pola prostokąta, którego dwa wierzchołki leżą na paraboli o równaniu
y=x2, a dwa pozostałe na cięciwie paraboli wyznaczonej przez prostą o równaniu y=3
B(x, 3) x>0 (x∊(0;
∞))
A(−x,3)
C(x,x
2)
D(−x, x
2)
|AB| =
√(x+x)2 = |2x
2| = 2x
2 bo x>0
|AD| =
√(−x+x)2+(x2−3)2=
√(x2−3)2 (i co tutaj zrobić? żeby to opuścić nie zmieniając
znaku musiałbym dać inne założenie x)
x∊(−
∞; −
√3) U (
√3;
∞)
P(x) = 2x
2(x
2−3) = 2x
4−6x
2
P'(x) = 8x
3−12x
P'(x)=0 ⇔ 8x
3−12x=0
8x
3−12x=0
4x(2x
2−3)=0
x=0 v x= −
√3 v x=
√3
I z wykresu pochodnej wychodzi na to, że wartość największa nie jest określona, bo w przedziale
(
√3;
∞) funkcja rośnie
31 sty 19:17
salamandra:
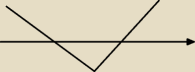
Ok, znalazłem pierwszy błąd− w AB powinno być 2x, ale to i tak
P(x)= 2x(x
2−3)=2x
3−6x
P'(x)= 6x
2−6
P'(x)=0 ⇔ 6x
2−6 =0
6x
2−6=0
x
2=1
x=−1 v x=1
Przepraszam za tak ostrą "parabolę", ale nie mogłem jej narysować.
Z tego wynika że −1 jest lokalnym maksimum, a w odpowiedzi jest, że to dla x=1 będzie
największe pole
31 sty 19:30
Mila:
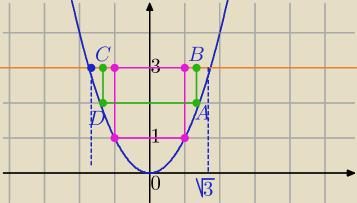
y=x
2
x
2=3
x=
√3 lub x=−
√3
B=(x,3), C=(−x,3) x∊(−
√3,
√3)
A=(x,y), x∊(0,
√3 ), D=(−x,y), y∊(0,3), y=x
2
|AB|=
√(3−y)2=|3−y|=3−y
|AD|=2x
P(x)=2x(3−x
2)
P(x)=6x−2x
3
P'(x)=6−6x
2
6−6x
2=0
1−x
2=0
x=1 lub x=−1
1−x
2>0⇔x∊(−1,1) i x>0
w x=1 maksimum, przy przejściu przez x=1 pochodna zmienia znak z (+) na (−)
31 sty 20:36
salamandra: Dziękuję bardzo

, nawiasem − czy widzisz, abym gdzieś popełnił błąd logiczny?
31 sty 20:47
Mila:
Masz niedobry rysunek, (19.17) prosta y=3 ma ograniczać prostokąt od góry,
a u Ciebie prostokąt jest nieograniczony od góry i dlatego Ci nie wychodzi.
31 sty 20:54
salamandra: A skąd wynika, które wierzchołki mają być "górne"?
31 sty 20:57
salamandra: Bo wtedy pole mogłoby być nieskończenie wielkie?
31 sty 21:03
Mila:
Tak , prostokąt nie miałby ograniczenia z góry.
31 sty 21:24
Jerzy:
Awesome

31 sty 21:51
salamandra: Jeszcze w sumie jedno pytanie− do |AD|, skoro x∊(−√3; √3) to dlaczego piszemy, że to 2x,
skoro to √(2x)2, więc |2x|, i nie wiemy jaki jest x?
31 sty 22:28
salamandra: Ok, nieważne, nie zauważyłem klauzuli x∊(0; √3)
31 sty 22:30
salamandra: Tylko nie wiem, bo dla B i C zakładamy przedział (−√3; √3) (są one symetryczne tak jak A i
D), a dla A i D zakładamy (0;√3)?
31 sty 22:34
salamandra: Podbiję, bo to dość istotna dla mnie wątpliwość
3 lut 11:48
 y=−x2+4
B=(x,4−x2), C=(−x, −x2+4)
A=(x,0), x>0, bo A leży po prawej stronie OY
D=(−x,0)
|AD|=|2x|=2x, |AD|=|BC|
|AB|=√(−x2+4)2=−x2+4 dla x>0 i x<2 bo punkt A nie może leżeć poza wykresem
P▭=|AD|*|AB|=2x*(−x2+4)
=======================
Może obliczyć tyko pole prostokąta po prawej i pomnożyc przez 2 (symetria)
albo policzyć P1 i pole po lewej wtedy:
P(x)=P1(x)+P2(x) ale po co ?
y=−x2+4
B=(x,4−x2), C=(−x, −x2+4)
A=(x,0), x>0, bo A leży po prawej stronie OY
D=(−x,0)
|AD|=|2x|=2x, |AD|=|BC|
|AB|=√(−x2+4)2=−x2+4 dla x>0 i x<2 bo punkt A nie może leżeć poza wykresem
P▭=|AD|*|AB|=2x*(−x2+4)
=======================
Może obliczyć tyko pole prostokąta po prawej i pomnożyc przez 2 (symetria)
albo policzyć P1 i pole po lewej wtedy:
P(x)=P1(x)+P2(x) ale po co ?
 Dlatego, skoro założę x<0 i D(x,0), to A będzie miało x "przeciwny", czyli −x?
Ok, idąc do tego ćwiczenia:
Oblicz największą wartość pola prostokąta, którego dwa wierzchołki leżą na paraboli o równaniu
y=x2, a dwa pozostałe na cięciwie paraboli wyznaczonej przez prostą o równaniu y=3
B(x, 3) x>0 (x∊(0;∞))
A(−x,3)
C(x,x2)
D(−x, x2)
|AB| = √(x+x)2 = |2x2| = 2x2 bo x>0
|AD| = √(−x+x)2+(x2−3)2= √(x2−3)2 (i co tutaj zrobić? żeby to opuścić nie zmieniając
znaku musiałbym dać inne założenie x)
x∊(−∞; −√3) U (√3; ∞)
P(x) = 2x2(x2−3) = 2x4−6x2
P'(x) = 8x3−12x
P'(x)=0 ⇔ 8x3−12x=0
8x3−12x=0
4x(2x2−3)=0
x=0 v x= −√3 v x=√3
I z wykresu pochodnej wychodzi na to, że wartość największa nie jest określona, bo w przedziale
(√3; ∞) funkcja rośnie
Dlatego, skoro założę x<0 i D(x,0), to A będzie miało x "przeciwny", czyli −x?
Ok, idąc do tego ćwiczenia:
Oblicz największą wartość pola prostokąta, którego dwa wierzchołki leżą na paraboli o równaniu
y=x2, a dwa pozostałe na cięciwie paraboli wyznaczonej przez prostą o równaniu y=3
B(x, 3) x>0 (x∊(0;∞))
A(−x,3)
C(x,x2)
D(−x, x2)
|AB| = √(x+x)2 = |2x2| = 2x2 bo x>0
|AD| = √(−x+x)2+(x2−3)2= √(x2−3)2 (i co tutaj zrobić? żeby to opuścić nie zmieniając
znaku musiałbym dać inne założenie x)
x∊(−∞; −√3) U (√3; ∞)
P(x) = 2x2(x2−3) = 2x4−6x2
P'(x) = 8x3−12x
P'(x)=0 ⇔ 8x3−12x=0
8x3−12x=0
4x(2x2−3)=0
x=0 v x= −√3 v x=√3
I z wykresu pochodnej wychodzi na to, że wartość największa nie jest określona, bo w przedziale
(√3; ∞) funkcja rośnie
 Ok, znalazłem pierwszy błąd− w AB powinno być 2x, ale to i tak
P(x)= 2x(x2−3)=2x3−6x
P'(x)= 6x2−6
P'(x)=0 ⇔ 6x2−6 =0
6x2−6=0
x2=1
x=−1 v x=1
Przepraszam za tak ostrą "parabolę", ale nie mogłem jej narysować.
Z tego wynika że −1 jest lokalnym maksimum, a w odpowiedzi jest, że to dla x=1 będzie
największe pole
Ok, znalazłem pierwszy błąd− w AB powinno być 2x, ale to i tak
P(x)= 2x(x2−3)=2x3−6x
P'(x)= 6x2−6
P'(x)=0 ⇔ 6x2−6 =0
6x2−6=0
x2=1
x=−1 v x=1
Przepraszam za tak ostrą "parabolę", ale nie mogłem jej narysować.
Z tego wynika że −1 jest lokalnym maksimum, a w odpowiedzi jest, że to dla x=1 będzie
największe pole
 y=x2
x2=3
x=√3 lub x=−√3
B=(x,3), C=(−x,3) x∊(−√3,√3)
A=(x,y), x∊(0,√3 ), D=(−x,y), y∊(0,3), y=x2
|AB|=√(3−y)2=|3−y|=3−y
|AD|=2x
P(x)=2x(3−x2)
P(x)=6x−2x3
P'(x)=6−6x2
6−6x2=0
1−x2=0
x=1 lub x=−1
1−x2>0⇔x∊(−1,1) i x>0
w x=1 maksimum, przy przejściu przez x=1 pochodna zmienia znak z (+) na (−)
y=x2
x2=3
x=√3 lub x=−√3
B=(x,3), C=(−x,3) x∊(−√3,√3)
A=(x,y), x∊(0,√3 ), D=(−x,y), y∊(0,3), y=x2
|AB|=√(3−y)2=|3−y|=3−y
|AD|=2x
P(x)=2x(3−x2)
P(x)=6x−2x3
P'(x)=6−6x2
6−6x2=0
1−x2=0
x=1 lub x=−1
1−x2>0⇔x∊(−1,1) i x>0
w x=1 maksimum, przy przejściu przez x=1 pochodna zmienia znak z (+) na (−)
 , nawiasem − czy widzisz, abym gdzieś popełnił błąd logiczny?
, nawiasem − czy widzisz, abym gdzieś popełnił błąd logiczny?
