Parametr m, cztery rozwiązania. Źle rozwiązane Pat: Witam, mam problem z zadaniem: Dla jakiej wartości parametru m równanie ma cztery różne rozwiązania? x⁴+mx²+m+2=0 Moje rozwiązanie: Jeżeli wielomian W(x)=x⁴+mx²+m+2 ma 4 pierwiastki to można go zapisać jako: (x−a)(x−b)(x−c)(x−d), gdzie a,b,c,d to pierwiastki tego wielomianu. Po wymnożeniu nawiasów dostałem: x⁴+x³(−a−b−c−d)+x²(ac+ad+bd+cd)+x(−ac−ad−acd−bcd)+abcd (okropne bardzo) Powyższy wielomian równa się W(x) kiedy współczynniki przy tych samych potęgach są sobie równe, więc: Układ równań: −a−b−c−d=0 ac+ad+bd+cd=m (2) −ac−ad−acd−bcd=0 abcd=m+2 Mogę jedynie jeszcze (2) przekształcić: a(c+d)+b(c+d)+cd=(cd)(ab)+cd I tu utknąłem. Proszę o pomoc. Chyba źle się to tego zadania zabrałem. W odpowiedziach jest: m∊(−2;2−2√3)

ABC: wprowadź zmienną pomocniczą t=x² otrzymasz równanie t²+mt+m+2=0 musi ono mieć dwa różne pierwiastki dodatnie delta= m²−4(m+2)=m²−4m−8>0 m²−4m+4−12>0 (m−2)²>12 (m−2)²>(2√3)² m−2∊(−∞,−2√3) lub m−2∊(2√3,+∞) i dorzuć warunek zw wzorów Viete'a suma i iloczyn pierwiastków większy od zera

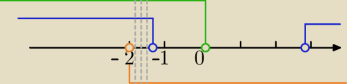
Mila: x⁴+mx²+m+2=0 x²=t, t²+mt²+m+2=0 (Δ>0 ⋀ t₁+t₂>0 ⋀t₁*t₂>0) 1) Δ=m²−4m−8>0 (m−2)²−12=0 m=2+2√3 lub m=2−2√3 ⇔Δ>0 dla (m<2−2√3 lub m>2+√3) i 2) t₁+t₂=−m >0⇔m<0 i 3)t₁*t₂=m+2>0⇔m>−2 (1) i (2) i (3) ⇔m∊(−2,2−2√3) ========================

Pat: Super dzięki. Wszystko rozumiem. Niestety mój mózg nie chce czasem wprowadzać zmiennej pomocniczej aby sobie pomóc.

Mila: