

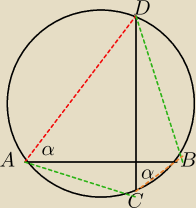
 Domyślam sie, ze jakos z tw. sinusów to trzeba, ale co dalej?
Domyślam sie, ze jakos z tw. sinusów to trzeba, ale co dalej?
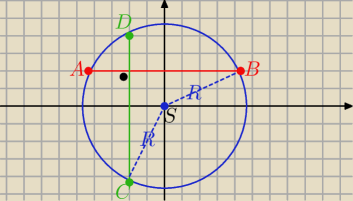 Podam taki sposób:
Z wykorzystaniem geometrii analitycznej
Umieszczam środek okręgu w punkcie S(0,0)
A(−x,y) , B( x,y) , C( −m,−n) , D(−m,n)
x2+y2=m2+n2=R2
|AC|2=(x−m)2+(y+n)2= x2−2mx+m2+y2+2ny+n2= 2R2−2mx+2ny
|DB|2=(x+m)2+(y−n)2= x2+2mx+m2+y2−2ny+y2= 2R2+2mx−2ny
i ... mamy tezę
|AC|2+|DB|2= 4R2
================
Podam taki sposób:
Z wykorzystaniem geometrii analitycznej
Umieszczam środek okręgu w punkcie S(0,0)
A(−x,y) , B( x,y) , C( −m,−n) , D(−m,n)
x2+y2=m2+n2=R2
|AC|2=(x−m)2+(y+n)2= x2−2mx+m2+y2+2ny+n2= 2R2−2mx+2ny
|DB|2=(x+m)2+(y−n)2= x2+2mx+m2+y2−2ny+y2= 2R2+2mx−2ny
i ... mamy tezę
|AC|2+|DB|2= 4R2
================
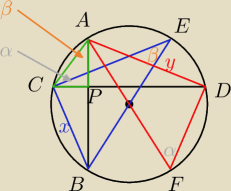 Bez tw. sinusów
1. Dorysowuję średnicę BE →ΔBCE jest prostokątny
2. Dorysowuję średnicę AF →ΔADF jest prostokątny
3. Niech kąt AFD=α, zatem kąt DCA=α (kąty oparte na tym samym łuku AD)
4. Niech kąt BEC=β, zatem kąt CAB=β (kąty oparte na tym samym łuku CB)
Bez tw. sinusów
1. Dorysowuję średnicę BE →ΔBCE jest prostokątny
2. Dorysowuję średnicę AF →ΔADF jest prostokątny
3. Niech kąt AFD=α, zatem kąt DCA=α (kąty oparte na tym samym łuku AD)
4. Niech kąt BEC=β, zatem kąt CAB=β (kąty oparte na tym samym łuku CB)
| x | ||
5. W ΔBCE mamy sinβ= | →x=2Rsinβ | |
| 2R |
| y | ||
6. W ΔADF mamy sinα= | →y=2Rsinα | |
| 2R |
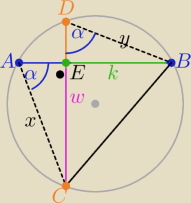 3 sposób
1/ rys.
2/ w trójkątach prostokątnych ACE i BED i BCE
w=x*sinα i k=y*sinα i |CB|2=w2+k2= (x2+y2)*sin2α
oraz |CB|=2R*sinα to |CB|2=4R2sin2α
i mamy tezę
x2+y2=4R2
|AC|2+|DB|2=4R2
================
3 sposób
1/ rys.
2/ w trójkątach prostokątnych ACE i BED i BCE
w=x*sinα i k=y*sinα i |CB|2=w2+k2= (x2+y2)*sin2α
oraz |CB|=2R*sinα to |CB|2=4R2sin2α
i mamy tezę
x2+y2=4R2
|AC|2+|DB|2=4R2
================
 Saizou− ale x i y, to nie są AC i DB, a to trzeba było udowodnić?
Saizou− ale x i y, to nie są AC i DB, a to trzeba było udowodnić?
