Stereometria Lili: W stożku o kącie rozwarcia dwa Alfa mieści się drugi Stożek o wspólnej z nim osi. Wierzchołek drugiego stożka znajduje się w środku podstawy pierwszego. Kąt rozwarcia drugiego stożka wynosi 2 beta. Oblicz stosunek pól powierzchni bocznych obu stożków.

wmboczek: wyszło mi sin²(α+β)/(sinαsinβ) ale nie jestem pewnien bo w pośpiechu robiłem

Mila: Mam inny wynik, sprawdzam swoje rachunki. Ty też sprawdź.

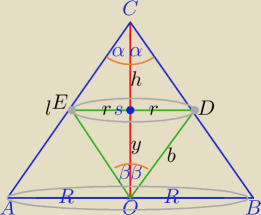
Mila: |CO|=H=h+y

	πR*l		R*l
s=		⇔ (*) s=
	πr*b		r*b

1) W ΔCSD:

	h
ctgα=		⇔h=r*ctgα
	r

2) W DSO:

	y
ctgβ=		⇔y=r*ctgβ
	r

	r		r
sinβ=		⇔b=
	b		sinβ

3) H=h+y=r(ctgα+ctgβ) W ΔCOB:

	R
tgα=		⇔R=H*tgα⇔R=r*tgα*(ctgα+ctgβ)
	H

	H		H		r(ctgα+ctgβ)
cosα=		⇔l=		=
	l		cosα		cosα

4) podstawiam do wzoru (*)

	r(ctgα+ctgβ)   r*tgα*(ctgα+ctgβ)*   cosα
s=		=
	r   r*   sinβ

	sinβ*tgα*(ctgα+ctgβ)2
s=
	cosα

Pewnie można to jeszcze jakoś przekształcić .

wmboczek: zgadza się teraz, źle skróciłem sin²(α+β)/(sinαsinβcos²α) co odpowiada wynikowi @Mila

Mila: Myślę, że jest krótszy sposób. Może jeszcze coś pomyślę Dziękuję wmboczek za odpowiedź. Maturzyści wpisują zadania i nie zaglądają do rozwiązań