Bryły ABC: W kulę o promieniu R wpisano stożek którego tworząca jest widoczna ze środka kuli pod kątem Alfa wyznacz pole powierzchni całkowitej i objętość stożka.

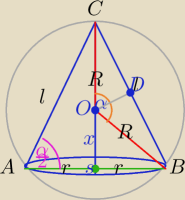
Mila: 1) W ΔCDO:

	α		1   2		α
sin		=		⇔ l=2R*sin
	2		R		2

2)

	α
∡A=		Jako kąt wpisany oparty na tym samym co kąt środkowy COB=α
	2

W ΔASC:

	α		r
cos		=
	2		l

	α		α		α
r=l*cos		=2Rsin		*cos		⇔ r=Rsinα
	2		2		2

	α		|SC|
sin		=
	2		l

	α		α
|SC|=H=lsin		=2Rsin2
	2		2

	1		α
V=		πR2*sin2α*2Rsin2
	3		2

	2π		α
V=		R3*sin2α*2Rsin2
	3		2

P_c=πr²+πrl licz sam ====================

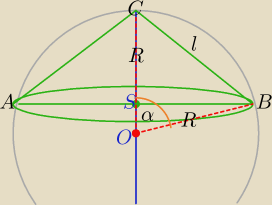Mila: II przypadek Środek podstawy stożka leży powyżej środka kuli ( kąt rozwarcia stożka − kąt rozwarty) spróbuj sam obliczyć III przypadek Środek podstawy stożka pokrywa się ze środkiem kuli. Objętość stożka jest 4 razy mniejsza niż objętość kuli.

	1
Vs=		πR3 ale to samo otrzymasz podstawiając do wzoru na V z godziny 16:14.
	3

Tam trzeba poprawić:

	2π		α
V=		R3 sin2α*sin2(		)
	3		2

=========================== Po kopiowaniu nie usunęłam 2.