własności trójkąta zgredek95: Funkcja wykładnicza f określona jest wzorem f(x) = 4x, dla każdego x ∈ R. Na wykresie funkcji g zdefiniowanej następująco: g(x) = f(x – 1) + 2, gdzie x ∈ R, wyznacz taki punkt C, aby trójkąt o wierzchołkach A=(log₂√2, 0), B= (1/2 log₂ 512, 0) i C, miał pole powierzchni równe 20.

Bleee: A co ma punkt C do funkcji?

janek191: Powinno być f(x) = 4^x

	1
A = (		, 0)
	2

	9
B = (		, 0)
	2

g(x) = f(x −1) + 2 = 4^{x −1} + 2 C = ( x, 4^x−1 + 2 )

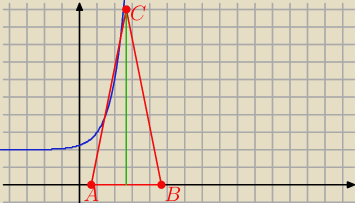
janek191: I AB I = 4,5 − 0,5 = 4 P = 0,5 *4*h = 20 ⇒ h = 10 4^{x −1} + 2 = 10 4 ^{x −1} = 8

1
	*4x = 8 /*4
4

4^x = 16*2 x = 2,5 C = ( 2,5 ; 10) =============