geometria Dominik: W czworokącie wypukłym ABCD boki AB i BC oraz AD i DC są prostopadłe. Wyznacz długość przekątnej AC wiedząc, że |CB| = a i |CD| = b oraz ∡BAD = 60 stopni. Jedyny mój wniosek taki, że ∡BCD = 120 stopni

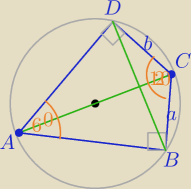
Mila: 1) Na czworokącie można opisać okrąg− sumy miar kątów przeciwległych mają po180^o 2) |DB|²=a²+b²−2*a*b*cos120^o |DB|²=a²+b²+ab |DB|=√a²+b²+ab 3) Z tw sinusów w ΔABD:

DB|
	=2R=|AC|
sin60

	√a2+b2+ab
|AC|=
	√3   2

	2√a2+b2+ab
|AC|=
	√3

a@b: 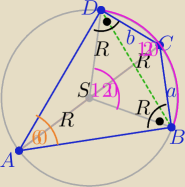2 sposób Z tw. cosinusów w trójkątach BSD i BCD , DC−− bok wspólny to R²+R²+RR = a²+b²+ab ⇒ 3R²=a²+b²+ab

	√a2+b2+ab
to R=
	√3

	2√a2+b2+ab
|AC|=2R=
	√3

======================

Dominik: Okej, dzięki. Wrócę sobie do tego jak będę coś więcej wiedział z trygonometrii niż jakieś podstawy