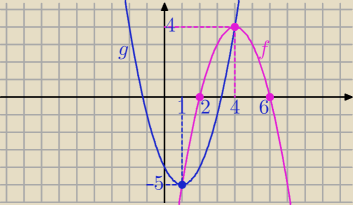
Funkcja kwadratowa f przyjmuje wartość największą równą 4 i olgaa: Funkcja kwadratowa f przyjmuje wartość największą równą 4 i ma dwa miejsca zerowe równe 2 i 6. Parabola będąca wykresem funkcji kwadratowej g, ma wierzchołek w punkcie należącym do wykresu funkcji f i przechodzi przez wierzchołek paraboli będącej wykresem funkcji kwadratowej f (zobacz rysunek https://imgur.com/mpy0Y58 ). Wyznacz wzór funkcji g w postaci ogólnej.

Eta:

	2+6
xw=p=		=4 , yw=q=4 to Wf(4,4)
	2

f(x)=a(x−2)(x−6) i W(4,4) 4=a(4−2)(4−6) ⇒ a= −1 f(x)=−(x−2)(x−6) W_g (1, f(1)) = (1,−5) to g(x)=a(x−1)²−5 i przechodzi przez W_f(4,4) to 4=a(4−1)²−5 ⇒ a=1 g(x)= (x−1)²−5 g(x)= x²−2x−4 ==============