Wykazanie, że suma długości kątów = 90 stopni
Kamil:
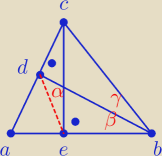
W trójkącie ostrokątnym ABC poprowadzono wysokości BD i CE. Wykaż, że
|∡ABC| + |∡BDE| = 90
o .
Mało danych w tym zadaniu i nic nie wymyśliłem. Będę wdzięczny za podpowiedź.

26 sty 21:27
an:
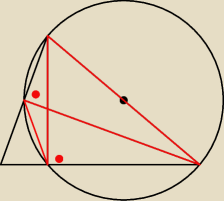
Mówi Ci to coś
26 sty 22:23
Mila:
Suma
miar kątów.!
|∡ABC| + |∡BDE| =? 90
o .
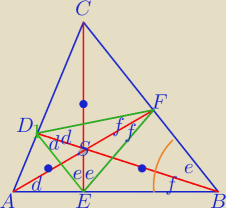
1) ΔDEF− trójkąt spodkowy ( poczytaj o tym na deltami.edu)
wysokości AF,BD,CF są dwusiecznymi kątów wewnętrznych ΔDEF
Na każdym z czworokątów:
AESD, EBFS, CDSF można opisać okrąg ( sumy miar kątów przeciwległych są równe 189
o)
Z tego wynika równość odpowiednich kątów wpisanych opartych na tym samym łuku.
Zaznaczyłam środki okręgów, zrób rysunek, to zobaczysz .
2d+2f+2e=180
o
d+e+f=90
o
cnw.
Zrobiłam rysunek, ale mało jest czytelny.
Jeśli sobie nie poradzisz , to jutro zrobię rysunek.
26 sty 23:01
Mila:
Może inny sposób ktoś dzisiaj poda.
Widzę, że an podała jeszcze inną propozycję, też z okręgiem.
26 sty 23:04
Kamil:
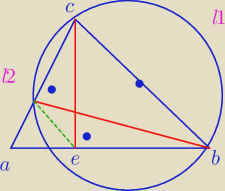
Oczywiście, że suma miar kątów. Głupi błąd.
Zapisałem taki dowód, ale nie wiem czy zrobiłem to dobrze. Gdyby ktoś mógł napisać czy na
maturze byłoby to dobre rozwiązanie to byłbym wdzięczny

Dowód:
L1=2πr * 180
o/360
o=2πr*1/2=πr=L2
Łuk L2 to 1/2 długości całego okręgu.
|∡BDE| oparty jest o część łuku L2 gdzie długość części łuku L2, na której oparty jest |∡BDE|
równa jest πr*α/180
o.
|∡EBC|=|∡ABC|
|∡EBC| oparty jest o część łuku L2 gdzie długość części łuku L2, na której oparty jest |∡EBC|
równa jest πr*180
o−α/180
o.
Suma długości łuków, na których oparte są 2 powyższe kąty:
πr*α/180
o+πr*180−α/180
o=πrα+180πr−πrα/180
o=180πr/180
o=πr=L2 ==> Kąt |∡EBC|+|∡BDE| jest
oparty o łuk będący 1/2 całego okręgu ==> Skoro |∡EBC|=|∡ABC| to |∡ABC|+|∡BDE|=90
o c.n.u
27 sty 21:05
Mila:
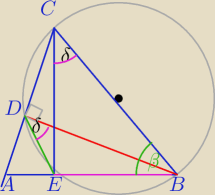
1) Szukasz kątów wpisanych na tym samym łuku.
kąty ∡EDB i ∡ECB są oparte na tym samym łuku EB , zatem są równe.
δ+β=90
o
Koniec

27 sty 21:40
Mila:
Podziękuj
an 
27 sty 21:42
Kamil: Ehh... Rysunek źle zrobiłem.

Na rysunku an widać, że punkt E należy do okręgu opisanego.
Poprawię później rysunek jeśli ten dowód okaże się prawidłowy
27 sty 21:43
Kamil: Dziękuję!

27 sty 21:44
Kamil: Korzystając z okazji zadam pytanie odnośnie mojego dowodu. Czy mogę zawierać w dowodach
twierdzenie właśnie takie, że suma kątów opartych łącznie o 1/2 długości okręgu jest równa
90o czy takie twierdzenie działa tylko dla jednego kąta?
27 sty 21:49
Mila:
Kąt wpisany oparty na półokręgu jest kątem prostym.
albo
Kąt wpisany oparty na średnicy jest kątem prostym.
27 sty 22:06
Kamil:
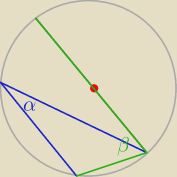
Nie wiem czy dobrze mnie zrozumiałaś więc zapytam jeszcze raz dla pewności

Tutaj α+β≠90
o,
tak?
27 sty 22:37
Mila:
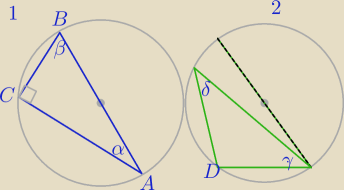
Ważne, abyś Ty zrozumiał co ja piszę.
1) α+β=90
o bo |∡ C|=90
o i z sumy kątów w Δ⇒ α+β=90
o
∡ C− kąt wpisany oparty na średnicy jest kątem prostym.
2) |∡ D|≠90
o to γ+δ≠90
o
27 sty 22:50
Kamil: Rozumiem

Dziękuję bardzo za pomoc kolejny raz
27 sty 22:57
 W trójkącie ostrokątnym ABC poprowadzono wysokości BD i CE. Wykaż, że
|∡ABC| + |∡BDE| = 90o .
Mało danych w tym zadaniu i nic nie wymyśliłem. Będę wdzięczny za podpowiedź.
W trójkącie ostrokątnym ABC poprowadzono wysokości BD i CE. Wykaż, że
|∡ABC| + |∡BDE| = 90o .
Mało danych w tym zadaniu i nic nie wymyśliłem. Będę wdzięczny za podpowiedź. 
 Mówi Ci to coś
Mówi Ci to coś
 Suma miar kątów.!
|∡ABC| + |∡BDE| =? 90o .
1) ΔDEF− trójkąt spodkowy ( poczytaj o tym na deltami.edu)
wysokości AF,BD,CF są dwusiecznymi kątów wewnętrznych ΔDEF
Na każdym z czworokątów:
AESD, EBFS, CDSF można opisać okrąg ( sumy miar kątów przeciwległych są równe 189o)
Z tego wynika równość odpowiednich kątów wpisanych opartych na tym samym łuku.
Zaznaczyłam środki okręgów, zrób rysunek, to zobaczysz .
2d+2f+2e=180o
d+e+f=90o
cnw.
Zrobiłam rysunek, ale mało jest czytelny.
Jeśli sobie nie poradzisz , to jutro zrobię rysunek.
Suma miar kątów.!
|∡ABC| + |∡BDE| =? 90o .
1) ΔDEF− trójkąt spodkowy ( poczytaj o tym na deltami.edu)
wysokości AF,BD,CF są dwusiecznymi kątów wewnętrznych ΔDEF
Na każdym z czworokątów:
AESD, EBFS, CDSF można opisać okrąg ( sumy miar kątów przeciwległych są równe 189o)
Z tego wynika równość odpowiednich kątów wpisanych opartych na tym samym łuku.
Zaznaczyłam środki okręgów, zrób rysunek, to zobaczysz .
2d+2f+2e=180o
d+e+f=90o
cnw.
Zrobiłam rysunek, ale mało jest czytelny.
Jeśli sobie nie poradzisz , to jutro zrobię rysunek.
 Oczywiście, że suma miar kątów. Głupi błąd.
Zapisałem taki dowód, ale nie wiem czy zrobiłem to dobrze. Gdyby ktoś mógł napisać czy na
maturze byłoby to dobre rozwiązanie to byłbym wdzięczny
Oczywiście, że suma miar kątów. Głupi błąd.
Zapisałem taki dowód, ale nie wiem czy zrobiłem to dobrze. Gdyby ktoś mógł napisać czy na
maturze byłoby to dobre rozwiązanie to byłbym wdzięczny  Dowód:
L1=2πr * 180o/360o=2πr*1/2=πr=L2
Łuk L2 to 1/2 długości całego okręgu.
|∡BDE| oparty jest o część łuku L2 gdzie długość części łuku L2, na której oparty jest |∡BDE|
równa jest πr*α/180o.
|∡EBC|=|∡ABC|
|∡EBC| oparty jest o część łuku L2 gdzie długość części łuku L2, na której oparty jest |∡EBC|
równa jest πr*180o−α/180o.
Suma długości łuków, na których oparte są 2 powyższe kąty:
πr*α/180o+πr*180−α/180o=πrα+180πr−πrα/180o=180πr/180o=πr=L2 ==> Kąt |∡EBC|+|∡BDE| jest
oparty o łuk będący 1/2 całego okręgu ==> Skoro |∡EBC|=|∡ABC| to |∡ABC|+|∡BDE|=90o c.n.u
Dowód:
L1=2πr * 180o/360o=2πr*1/2=πr=L2
Łuk L2 to 1/2 długości całego okręgu.
|∡BDE| oparty jest o część łuku L2 gdzie długość części łuku L2, na której oparty jest |∡BDE|
równa jest πr*α/180o.
|∡EBC|=|∡ABC|
|∡EBC| oparty jest o część łuku L2 gdzie długość części łuku L2, na której oparty jest |∡EBC|
równa jest πr*180o−α/180o.
Suma długości łuków, na których oparte są 2 powyższe kąty:
πr*α/180o+πr*180−α/180o=πrα+180πr−πrα/180o=180πr/180o=πr=L2 ==> Kąt |∡EBC|+|∡BDE| jest
oparty o łuk będący 1/2 całego okręgu ==> Skoro |∡EBC|=|∡ABC| to |∡ABC|+|∡BDE|=90o c.n.u
 1) Szukasz kątów wpisanych na tym samym łuku.
kąty ∡EDB i ∡ECB są oparte na tym samym łuku EB , zatem są równe.
δ+β=90o
Koniec
1) Szukasz kątów wpisanych na tym samym łuku.
kąty ∡EDB i ∡ECB są oparte na tym samym łuku EB , zatem są równe.
δ+β=90o
Koniec

 Na rysunku an widać, że punkt E należy do okręgu opisanego.
Poprawię później rysunek jeśli ten dowód okaże się prawidłowy
Na rysunku an widać, że punkt E należy do okręgu opisanego.
Poprawię później rysunek jeśli ten dowód okaże się prawidłowy

 Nie wiem czy dobrze mnie zrozumiałaś więc zapytam jeszcze raz dla pewności
Nie wiem czy dobrze mnie zrozumiałaś więc zapytam jeszcze raz dla pewności  Tutaj α+β≠90o,
tak?
Tutaj α+β≠90o,
tak?
 Ważne, abyś Ty zrozumiał co ja piszę.
1) α+β=90o bo |∡ C|=90o i z sumy kątów w Δ⇒ α+β=90o
∡ C− kąt wpisany oparty na średnicy jest kątem prostym.
2) |∡ D|≠90o to γ+δ≠90o
Ważne, abyś Ty zrozumiał co ja piszę.
1) α+β=90o bo |∡ C|=90o i z sumy kątów w Δ⇒ α+β=90o
∡ C− kąt wpisany oparty na średnicy jest kątem prostym.
2) |∡ D|≠90o to γ+δ≠90o
 Dziękuję bardzo za pomoc kolejny raz
Dziękuję bardzo za pomoc kolejny raz