geometria salamandra: Punkty A(−7,−2) i B(4,−7) są wierzchołkami podstawy trójkąta równoramiennego ABC, a wysokość opuszczona z wierzchołka A tego trójkąta zawiera się na prostej o równaniu 2x+19y+52 = 0. Oblicz współrzędne wierzchołka C. 2x+19y+52=0 19y=−2x−52/ :19

	−2		52
y=		x−
	19		19

Wysokość jest pod kątem prostym, więc prosta BC (bok BC) jest prostopadły do tej wysokości,

	19
więc współczynnik kierunkowy tej prostej musi być =
	2

	19
równanie prostej BC:		(x−4)−7
	2

	19
y=		x−45
	2

I w tym miejscu nie wiem co dalej

salamandra: Mogę tak? |AC|² = (x+7)²+(y+2)² = x²+14x+49+y²+4y+4 |BC|² = (x−4)²+(y+7)² = x²−8x+16+y²+14y+49

	19		19
Skoro C(x,y) leży na prostej y=		x−45 to C(x,		x−45)
	2		2

i |AC|=|BC|, przyrównać to, wyliczyć x i potem y?

salamandra: Nieaktualne, wyszło z tego co napisałem

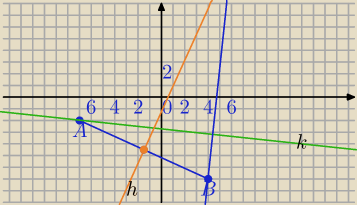
Mila: A(−7,−2) i B(4,−7) k: 2x+19y+52 = 0 1) wysokość opuszczona z wierzchołka C jest prostopadła AB i przechodzi przez środek AB (jest symetralną AB) (x+7)²+(y+2)²=(x−4)²+(y+7)²⇔ h: 11x−5y−6=0 2) k⊥BC i B∊prostej BC BC:

	19
y=		x−45 ⇔19x−2y−45=0
	2

Teraz szukasz punktu przecięcia z prostą h 19x−2y−45=0 11x−5y−6=0