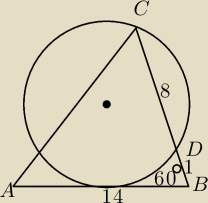
 Oblicz promień okręgu, który znajduje się na rysunku
Oblicz promień okręgu, który znajduje się na rysunku

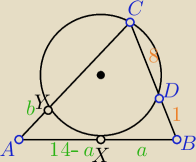 z twierdzenia o siecznych
1o |BD| * |BC| = |BX|2
oraz
2o |AX|2 = |AY| * |AC|
nazwijmy to "po ludzku"
czyli niech |BX| = a, wtedy |AX| =14 − a
analogicznie |AY| = b, zaraz znajdziemy |AC|
z tw. cosinusow znajdzmy |AC|:
|AC|2 = 82 + 142 − 2*8*14*cos(60)
z twierdzenia o siecznych
1o |BD| * |BC| = |BX|2
oraz
2o |AX|2 = |AY| * |AC|
nazwijmy to "po ludzku"
czyli niech |BX| = a, wtedy |AX| =14 − a
analogicznie |AY| = b, zaraz znajdziemy |AC|
z tw. cosinusow znajdzmy |AC|:
|AC|2 = 82 + 142 − 2*8*14*cos(60)
| 1 | ||
|AC|2 = 64+196 − 224 * | ||
| 2 |
| 121 | ||
112 = b * 2√37 −−−> b = | ||
| 2√37 |
| 121 | ||
|YC| = 2√37 − | ||
| 2√37 |
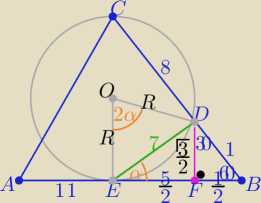 1/ z tw. o stycznej i siecznej : EB2=9*1 ⇒ EB=3
2/ z trójkąta BFD "ekierki" : FB=1/2 , FD=√3/2
to EF=5/2 i z tw. Pitagorasa w ΔEFD : ED=7
Kąt dopisany BED dwa razy mniejszy od kąta środkowego EOD
3/ w ΔFED : sinα= √3/14
cos(2α)= 1−2sin2α=......
W ΔEOD z tw. cosinusów
72=R2+R2−2R*r*cos(2α)
...................
R=................
1/ z tw. o stycznej i siecznej : EB2=9*1 ⇒ EB=3
2/ z trójkąta BFD "ekierki" : FB=1/2 , FD=√3/2
to EF=5/2 i z tw. Pitagorasa w ΔEFD : ED=7
Kąt dopisany BED dwa razy mniejszy od kąta środkowego EOD
3/ w ΔFED : sinα= √3/14
cos(2α)= 1−2sin2α=......
W ΔEOD z tw. cosinusów
72=R2+R2−2R*r*cos(2α)
...................
R=................
 Widzę błędny zapis
Powinno być : ED=√7
Widzę błędny zapis
Powinno być : ED=√7
| √21 | ||
zatem sinα= | ||
| 14 |