ars mathematica geometria płaska
asd:
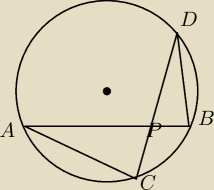
W okręgu poprowadzono cięciwy AB i CD,które przecięły się w punkcie P.Zakładamy,że
|PC|=|PD|,oraz |AP| = 9,|PD| = 4.Wówczas trójkąt APC jest podobny do trójkąta DPB w skali:
A.1,5
B.1,75
C.2
D.2.25
Autor w rozwiązaniu z tyłu książki zadania podaje,że |CP| = 6,a skoro zakładamy tak jak w
poleceniu,to przecież powinno być |CP| =|PD|= 4,potem z podobieństwa i wychodzi Odp.D z tego
co mi się wydaje.
Czy natknąłem się na błąd co w sumie nie byłoby dziwne bo człowiek popełnia błędy,czy coś
pomyliłem ?
