równanie trygonometryczne salamandra: Rozwiąż równanie:

	π		π		1
cosx[sin(x−		)+sin(x+		)] =		sinx
	3		3		2

	x−π3+x+π3		x−π3−x−π3		1
cosx[2sin(		)cos(		)] =		sinx
	2		2		2

	−π		1
cosx[(2sin(x)cos(		)] =		sinx
	3		2

	1
cosx*sinx =		sinx / *2
	2

2sinxcosx= sinx sin2x = sinx sin2x−sinx = 0

	3x		x
2cos		sin		=0
	2		2

3x		π		2		x
	=		+kπ / *		v sin		= 0
2		2		3		2

	π		2
x=		+		kπ v x=2kπ
	3		3

k∊C

	π		−π
Odpowiedź jest: x∊{kπ,		+2kπ,		+2kπ}
	3		3

Popełniłem gdzieś błąd, czy jest to równoważne?

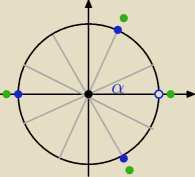Saizou : Te odpowiedzi są równoważne. Zobaczmy na koło trygonometryczne.

	π
α=
	6

Niebieskie punkty to Twoje rozwiązania Zielone to odpowiedzi z książki. Wszystko się zgadza