Dowód, że trapez jest równoramienny
Kamil:
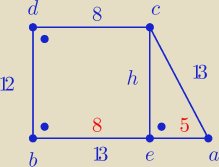
Wykaż, że trapez o podstawach długości 8 i 13 oraz ramionach długości 12 i 13 jest trapezem
prostokątnym.
Rozwiązałem to zadanie w ten sposób:
|BE|=|DC|=8
|EA|=13−8=5
W trapezie prostokątnym wysokość równa jest długości krótszego ramienia.
h
2+5
2=13
2
h
2=144 /
2
h=12 ==> Udowodniłem, że wysokość jest równa długości krótszego ramienia trapezu zatem trapez
ten jest prostokątny.
Czy to rozwiązanie jest poprawne? Czy mogłem tutaj narysować trapez prostokątny czy musiałem
narysować dowolny inny trapez i na podstawie tego innego trapezu udowodnić powyższą równość?
24 sty 18:11
Kamil: Opis zadania jest mylący. Chodziło tutaj o dowód, że trapez jest prostokątny

24 sty 18:21
ABC:
jak stosujesz Pitagorasa musisz udowodnić że masz kąt prosty
24 sty 18:58
Kamil: Wystarczyłoby zapisać, że wysokość jest odcinkiem łączącym wierzchołek trapezu z
naprzeciwległym bokiem pod kątem prostym?
24 sty 19:06
Kamil: Bo przyznam, że przy rysunku z dowolnym trapezem nie mam pomysłu jak udowodnić to, że ten
dowolny trapez o podanych miarach boków jest prostokątny
24 sty 19:12
Bleee:
Niestety nie jest to prawidłowe rozwiązanie bo już samym rysunkiem zakładasz ze jest to trapez
prostokątny.
Przy ogólnym rysunku trapezu robisz podobnie. Opuszczasz wysokości i masz dwa trójkąty
prostokatne:
1) o bokach h, x, oraz 12
2) o bokach h, 5−x oraz 13
Dwa tw. Pitagorasa, masz układ rownan z dwoma niewiadomymi. Odejmujac równanie otrzymujesz:
(5−x)2 − x2 = 132 − 122
(5−x − x)(5−x + x) = 25
(5 − 2x)*5 = 52 − > x = 0 − > h = 12
I teraz wniosek z powyższego, że wysokość równa jest krótszemu bokowi więc to trapez
prostokątny jest
24 sty 19:31
Kamil: Dziękuję bardzo. Wszystko jasne

24 sty 19:34
a@b:
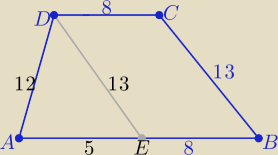
ΔAED o bokach długości : 12,13,5
jest trójkątem prostokątnym o przeciwprostokątnej 13
zatem |∡DEA|=90
o
Wniosek ........ trapez ABCD jest prostokątny
24 sty 19:53
a@b:
Poprawiam chochlika
zatem : |∡DAE|=90o
24 sty 19:57
Mila:
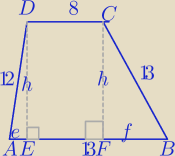
e+f=13−8, e+f=5
W ΔCFB: f
2=169−h
2
W ΔDEA: e
2=144−h
2
==========
f
2−e
2=25
(f−e)*(f+e)=25
(f−e)*5=25
f−e=5
f+e=5
===
2f=10
f=5⇔e=0
Wysokość DE pokrywa się z ramieniem AD.
Możesz jeszcze dopisać:
W ΔCFB : h=
√169−25
h=12
24 sty 20:23
a@b:

24 sty 20:41
a@b:
Który sposób najłatwiejszy ? i najkrótszy ?

Pozdrawiam całą brygadę niestrudzonych pasjonatów

24 sty 20:43
Mila:
Oczywiście Twój

24 sty 20:48
Mila:
Swój dopisałam, aby autor widział, że można inaczej.
24 sty 20:50
a@b:

24 sty 20:52
Kamil: Dziękuję raz jeszcze

24 sty 22:31
 Wykaż, że trapez o podstawach długości 8 i 13 oraz ramionach długości 12 i 13 jest trapezem
prostokątnym.
Rozwiązałem to zadanie w ten sposób:
|BE|=|DC|=8
|EA|=13−8=5
W trapezie prostokątnym wysokość równa jest długości krótszego ramienia.
h2+52=132
h2=144 /2
h=12 ==> Udowodniłem, że wysokość jest równa długości krótszego ramienia trapezu zatem trapez
ten jest prostokątny.
Czy to rozwiązanie jest poprawne? Czy mogłem tutaj narysować trapez prostokątny czy musiałem
narysować dowolny inny trapez i na podstawie tego innego trapezu udowodnić powyższą równość?
Wykaż, że trapez o podstawach długości 8 i 13 oraz ramionach długości 12 i 13 jest trapezem
prostokątnym.
Rozwiązałem to zadanie w ten sposób:
|BE|=|DC|=8
|EA|=13−8=5
W trapezie prostokątnym wysokość równa jest długości krótszego ramienia.
h2+52=132
h2=144 /2
h=12 ==> Udowodniłem, że wysokość jest równa długości krótszego ramienia trapezu zatem trapez
ten jest prostokątny.
Czy to rozwiązanie jest poprawne? Czy mogłem tutaj narysować trapez prostokątny czy musiałem
narysować dowolny inny trapez i na podstawie tego innego trapezu udowodnić powyższą równość?


 ΔAED o bokach długości : 12,13,5
jest trójkątem prostokątnym o przeciwprostokątnej 13
zatem |∡DEA|=90o
Wniosek ........ trapez ABCD jest prostokątny
ΔAED o bokach długości : 12,13,5
jest trójkątem prostokątnym o przeciwprostokątnej 13
zatem |∡DEA|=90o
Wniosek ........ trapez ABCD jest prostokątny
 e+f=13−8, e+f=5
W ΔCFB: f2=169−h2
W ΔDEA: e2=144−h2
==========
f2−e2=25
(f−e)*(f+e)=25
(f−e)*5=25
f−e=5
f+e=5
===
2f=10
f=5⇔e=0
Wysokość DE pokrywa się z ramieniem AD.
Możesz jeszcze dopisać:
W ΔCFB : h=√169−25
h=12
e+f=13−8, e+f=5
W ΔCFB: f2=169−h2
W ΔDEA: e2=144−h2
==========
f2−e2=25
(f−e)*(f+e)=25
(f−e)*5=25
f−e=5
f+e=5
===
2f=10
f=5⇔e=0
Wysokość DE pokrywa się z ramieniem AD.
Możesz jeszcze dopisać:
W ΔCFB : h=√169−25
h=12

 Pozdrawiam całą brygadę niestrudzonych pasjonatów
Pozdrawiam całą brygadę niestrudzonych pasjonatów


