Równanie trygonometryczne z parametrem Patryk: Cześć, Mam zadanie z trygonometrii i nie rozumiem jednej rzeczy. Dla jakich wartości parametru m równanie sin²x + sinx + m = 0 ma rozwiązania? Wiem, że trzeba rozpatrzeć dwa warunki. 1) Δ = 0 lub 2) Δ > 0 i g(1) ≥0 Dziedzina to będzie x∊<−1; 1> W 1) będę miał sytuacje dla jednego rozwiązania w 2) dla dwóch rozwiązan, ale dlaczego akurat g(1) ≥0? Nie powinno być jeszcze g(−1) ≥ 0 Bo te dwa miejsca zerowe mają się mieścić w przedziale <−1;1>.

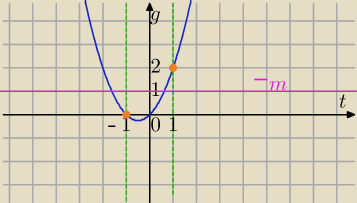
Mila: Metoda graficzna: 1) sin²x + sinx + m = 0⇔ sin²x+sinx=−m f(x)=sin²x+sinx, g(m)=−m sinx=t, t∊<−1,1> f(t)=t²+t interesuje nas zbór wartości g(t) wsp. wierzchołka paraboli

	1		1		1
tw=−		, f(−		)=−		− wartość najmniejsza f(t)
	2		2		4

f(1)=2− wartość największa f(t) 2)

	1
równanie : sin2x+sinx=−m posiada rozwiązanie dla (−m)∊<−		,2)
	4

	1		1
a) −m=−		⇔m=		− jedno rozwiązanie
	4		4

	1
b) −		<−m≤0 ⇔
	4

	1
dla 0≤m<		−dwa rozwiązania
	4

c) 0<−m≤2 ⇔ −2≤m<0 − jedno rozwiązanie

	1		1
d) −m<−		⇔m>		− brak rozwiązań
	4		4

−m>2⇔m<−2− brak rozwiązań

Patryk: Dzięki za rozpisanie i pomoc

Mila: