geometria analityczna trójkąt michaeli19: Punkt C = (−1, 4) jest wierzchołkiem trójkąta równoramiennego ABC, którego podstawa AB zawiera się w prostej o równaniu y − 2x + 4 = 0. znajdź współrzędne pozostałych wierzchołków trójkąta wiedząc, że długość podstawy AB jest równa długości wysokości tego trójkąta opuszczonej z wierzchołka C

salamandra: Wyznacz odległość punktu C od prostej− otrzymasz wysokość. Potem 1/2 AB do kwadratu + h² da ci AC² Później po otrzymaniu AC wstawiasz do wzoru na odległość dwóch punktów uwzględniając ze punkt A ma współrzędne (x,2x−4)

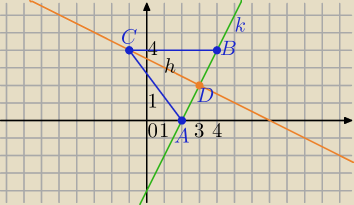
Mila: 1) k: − 2x +y+ 4 = 0. ⇔y=2x−4 C=(−1,4) h⊥k 2) Równanie prostej zawierającej wysokość

	1		1		7
y=−		x+b i 4=−		*(−1)+b⇔b=
	2		2		2

	1		7
h: y=−		x+
	2		2

D=(3,2) 3) długość wysokości h=√(3+1)²+(2−4)²=√20=2√5 4) |AD|=√5 (x−3)²+(y−2)²=(√5)² i y=2x−4 (x−3)²+(2x−6)²=5 x=2 lub x=4 Dokończ