Dwa zadania z którymi nie umiem sobie poradzić. kcmJ: Zad.1 Punkt B jest obrazem punktu A w jednokładności o środku w punkcie S i AB=4*SB. Skala s tej jednokładności spełnia warunek?

	1		1
Odp: −		≤ s ≤ −
	3		4

Prosiłbym o wytłumaczenie dlaczego. Zad.2 Spośród wszystkich liczb pięciocyfrowych wybieramy losowo jedną. Oblicz prawdopodobieństwo tego, że iloczyn cyfr wylosowanej liczby jest podzielny przez 8 i nie jest podzielny przez 16.

kcmJ: Zad. O to co stworzyłem: Z Z Z Z Z − pięciocyfrowa liczba. Z={0,1,2,3,4,5,6,7,8,9} |Ω| = 9*10*10*10*10=90 000 (bo na pierwszym miejscu nie może być zero, pozostałe dowolnie) Rozważamy przypadki, gdy iloczyn cyfr jest podzielny przez 8 i nie jest podzielny przez 16: a) jedna "8", pozostałe pięć cyfr nieparzystych 1*5*5*5*5=625 ("8" jedna możliwość, pozostałe z pięciu nieparzystych cyfr) 625*5=3125 (bo "8" może stać na pięciu różnych miejscach); b) z "4" mamy: "4" i "2" oraz "4" i "6" (inne kombinacje parzystych dzielą się przez 16 również, lub nie dzielą przez 8) − dla "4" i "2" 1*1*5*5*5=125 125*5*4=2 500 (bo "4" wybieramy na pięć sposobów, "2" na cztery lub odwrotnie, bez znaczenia) − dla "4" i "6" 1*1*5*5*5*5*4=2 500 (sytuacja analogiczna jak z "4" i "2") Łącznie 5 000 c) "2" i "6". Mamy: − trzy "2" (nie wiem jak zrobić dwumian Newtona, dlatego będę pisał [x nad y])* [5 nad 3]*5*5=250 (liczba kombinacji trzech "2" z dwumianu Newtona, pozostałe 2 miejsca na 5 sposobów nieparzystymi) − trzy "6" [5 nad 3]*5*5=250 (analogicznie jak dla trzech "2") − dwie "2" i "6" [5 nad2]*1*5*5*3=750 (razy 3 dlatego, że "6" na 3 sposoby, pozostałe logika jak wyżej) − dwie "6" i "2" [5 nad2]*1*5*5*3=750 (jak dla dwóch "2" i "6") Łącznie 2000 Sumujemy: |A|=3 125+ 5 000+ 2 000= 10 125

	10 125		9
P(A)=		=		(co jest zgodne z podaną odpowiedzią)
	90 000		80

Robiłem to według klucza i wszystkie wyniki starałem się uzyskać jakie powinny być, więc jeśli logika, którą sobie dodałem jest błędna prosiłbym o wskazanie tego.

	1		1
Ponawiam prośbę o zadanie pierwsze. W odpowiedzi powinno być −		≤ s < −
	3		4

kcmJ: b) z "4" mamy: "4" i "2" oraz "4" i "6" (inne kombinacje parzystych dzielą się przez 16 również, lub nie dzielą przez 8) − tu dodam jeszcze sprostowanie, że ograniczeniem jest tylko podzielność przez 16, bo chyba wszystkie dzielą się przez 8.*

ite: 10:05 proponuję taki sposób liczenia i zapis, może jest czytelniejszy a/ jedna "8", pozostałe cztery cyfry nieparzyste na dowolnym miejscu ósemka, na pozostałych dowolna z cyfr {1,3,5,7,9}

5 1
	na tyle sposobów wybieram miejsce dla ósemki

5⁴ na pozostałych czterech miejscach dowolna z pięciu cyfr {1,3,5,7,9}

	5 1
więc mamy		*54 = 3125

wyrażenie zapisujemy N {5}{1} bez spacji

kcmJ: Dzękuję, czyli chyba ogólnie dobrze zadanie 2. Z zapisem N {}{} zapamiętam. A jakiś pomysł z zadaniem pierwszym? Jak dojść do takiego wyniku?

ite:

	1
W pierwszym to wynik dla mnie może być nawet		: )) , więc też czekam aż ktoś to wyjaśni.
	5

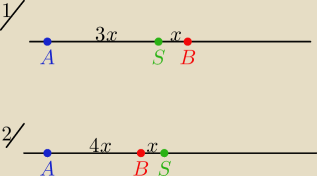
a@b: 1/ punkty A i B lezą po przeciwnych stronach S więc skala s<0

	x		1
s= −		= −
	3x		3

2/ Punkty A i B leżą po tej samej stronie punktu S więc skala s>0

	x		1
s=		=
	5x		5

kcmJ: Rozumiem. Tak jak w rozwiązaniu a@b, więc nie będę już powtarzał, informację AB=4*SB należy wykorzystać do określenia długości odcinków.

	1		1
Z punktu 1/ s=−		odnosi się do lewej strony warunku, natomiast z −		należy chyba
	3		4

	1		1
rozumieć, że skoro s <		, to tym bardziej od −		(taka zmyłka, ważna była tylko ta
	5		4

	1
informacja o −		, bo jeśli wymienić pozostałe odpowiedzi do wyboru: a)−4 ≤ s ≤ −3;
	3

	1		1
c)−		≤ s ≤		d) 3 ≤ s ≤ 4, to łatwiej wykluczyć, iż to nieprawda.)
	4		3

Dziękuję a@b.

kcmJ:

	1
Albo błąd w druku i powinno być s <		, już sam nie wiem, bo jak się zastanowiłem, to co
	5

	1
napisałem powyżej byłoby prawdą dla s >		...
	5

ite: thx a@b również : ))