ekstrema analiza: Wyznaczyc najmniejsza i najwieksza wartosc funkcji f(x,y,z)=x²+y²+z²+x+y+z na kuli {(x,y,z) : x²+y²+z² ≤3}. Wyznaczyc wszystkie punkty, w których wartosci najmniejsza i najwieksza sa osiagane. Moglbym poprosic o poszczegolne kroki co po kolei robic?

jc: f=(x+1/2)² + (y+1/2)² + (z+1/2)² − 3/4 f jest więc kwadratem odległości od (−1/2,−1/2,−1/2) pomniejszonym o 3/4. Wartość najmniejszą równą −3/4 funkcja f przyjmie w punkcie (−1/2,−1/2,−1/2). Wartość największą równą 6 funkcja f przyjmie w punkcie (1,1,1) (to najdalej położony punkt).

analiza: To wszystko? A gdzie tu jest ta kula?

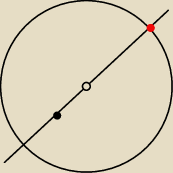
jc: Obrazek 2 wymiarowy. Prosta przechodzi przez czarną kropkę i przez środek. Czerwona kropka leży najdalej od czarnej.