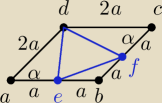
Romb i trójkąt jako część jego pola Kamil: Dany jest romb ABCD. Punkt E jest środkiem boku AB , a punkt F jest środkiem boku BC . Wyznacz, jaką częścią pola rombu jest pole trójkąta DEF . Zakoduj wynik podając trzy pierwsze cyfry po przecinku rozwinięcia dziesiętnego otrzymanego wyniku. 1. |∡DAE|=|∡DCF| więc ΔAED≡ΔDCF na podstawie cechy b−k−b. 2. PΔAED=PΔDCF 3. |DE|=|DF| więc ΔDEF jest równoramienny. Te 3 rzeczy udało mi się w tym zadaniu zobaczyć. Myślę, że do wykonania zadania potrzebne byłoby uzależnienie boków trójkąta DEF od zmiennej a. Możliwe, że dałoby się to zrobić opierając się o podobieństwo trójkąta DEF do któregoś z pozostałych trójkątów w tym rombie, ale ja tego nie widzę niestety. Ma ktoś pomysł co w dalszej kolejności powinienem zrobić? Byłbym wdzięczny za podpowiedź

janek191: Pole rombu P = 2a*2a sinα = 4 a² sin α Pole trzech trójkątów P₃Δ = 2*0,5*2a*a sinα + 0,5 a*a sin( 180^o −α) = 2 a² sin α + 0,5 a² sin α =2,5 a² sin α zatem P_Δ = 4 a² sin α − 2,5 a² sin α = 1,5 a² sin α oraz

PΔ		1,5		3
	=		=		= 0.375
P		4		8

Kamil: Dziękuję bardzo! Właściwie to zadanie nie było specjalnie trudne, ale brakło mi pomysłu ostatecznie

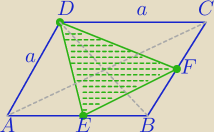Mila: P_ABCD=P

	1		1
1) PΔABD=		P, PΔAED=		PΔABD− Δ te mają tę samą wysokość⇒
	2		2

	1		1		1
PΔAED=		*		P=		P
	2		2		4

Analogicznie :

	1
PΔFCD=		P
	4

2)

	1
EB|| AC i |EB|=		|AC|
	2

	1
ΔEBF∼ΔACB w skali k=		⇔
	2

	1		1		1		1
PΔEBF=		PΔACB=		*		P=		P
	4		4		2		8

3)

	1		1
PΔEFD=P−(2*		P+		P)
	4		8

dokończ obliczenia