 a)
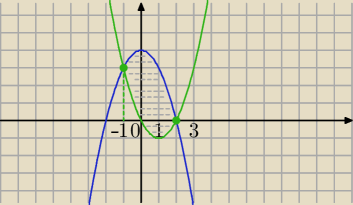
f(x)=4−x2
g(x)=x2−2x
4−x2=x2−2x
2x2−2x−4=0
x2−x−2=0
Δ=9
x1=−1 lub x2=2
a)
f(x)=4−x2
g(x)=x2−2x
4−x2=x2−2x
2x2−2x−4=0
x2−x−2=0
Δ=9
x1=−1 lub x2=2
| −2 | 1 | |||
P=−1∫2(4−x2−x2+2x)dx=−1∫2(−2x2+2x+4)dx=[ | x3+2* | x2+4x]−12= | ||
| 3 | 2 |
| 2 | 2 | 16 | 2 | |||||
=− | *8+4+8−( | +1−4)=− | +12− | +3=9 | ||||
| 3 | 3 | 3 | 3 |
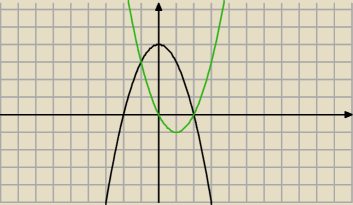 a) P = −1∫2[(4 − x2) − (x2 − 2)]dx
a) P = −1∫2[(4 − x2) − (x2 − 2)]dx
 b.)
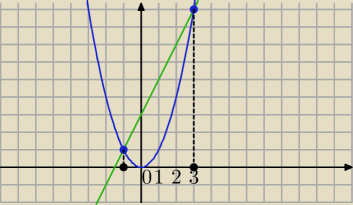
y = x2 i y = 2x + 3;
x2=2x+3
x2−2x−3=0
x=−1 lub x=3
P=−1∫3(2x+3−x2) dx= .. ?
Licz teraz sam.
b.)
y = x2 i y = 2x + 3;
x2=2x+3
x2−2x−3=0
x=−1 lub x=3
P=−1∫3(2x+3−x2) dx= .. ?
Licz teraz sam.