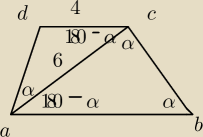
W trapezie ABCD boki |AB| i |CD| są podstawami oraz |CD| = 4, |AC| = 6. Ponadto
|<) DAC| = |<) ABC|. Wyznacz, jaką częścią pola trapezu ABCD jest pole trójkąta ACD.
Zakoduj wynik podając trzy pierwsze cyfry po przecinku rozwinięcia dziesiętnego
otrzymanego wyniku.
Wygląda na to, że pogubiłem się co do ustalenia odpowiednich kątów w opisanym trapezie.
Jestem pewny, że ∡DAC=∡ACB z kątów naprzemianległych. Z racji tego, że suma miar kątów
przyległych do jednego ramienia jest równa 180 stopni i, że suma miar kątów w trójkącie równa
jest
180 stopni to stwierdziłem, że ∡BAC=∡ACD (gdyby na rysunku nie było widać to ∡ACD=180−α)
Jednak wtedy ∡ADC=α, ale nie może tak być, ponieważ |CD| ≠ |AC| i nie może powstać trójkąt
równoramienny.
Z tego wynika, że mój tok myślenia odnośnie miar kątów jest błędny. Chciałbym Was prosić
o pomoc jak ruszyć to zadanie i dlaczego moje myślenie odnośnie miar tych kątów jest
niepoprawne.
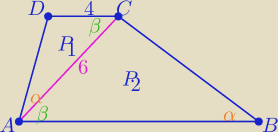Trójkąty ADC i ABC są podobne z cechy (kkk)
| 4 | 2 | |||
w skali k = | = | |||
| 6 | 3 |
| P1 | 4 | |||
to | =k2 ⇒ P1= | P2 | ||
| P2 | 9 |
| 13 | ||
P(ABCD)=P =P1+P2= | P2 | |
| 9 |
| P1 | 4 | ||
= | ≈0,30769 | ||
| P | 13 |
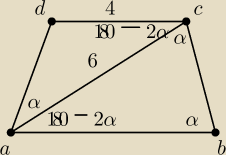Poprzednio źle narysowałem ten trapez 
W zeszycie te kąty mam oznaczone jako 180o−2α
oczywiście.
Mój tok myślenia: Skoro |∡DAC|=|∡ABC|=α to z kątów naprzemianległych |∡ACB|=|∡DAC|=α. Więc
ΔABC jest równoramienny i |AB|=|AC|=6. Suma miar kątów w trójkącie wynosi 180o więc
|∡BAC|=180o−2α. Z kątów naprzemianległych |∡ACD|=|∡BAC|=180o−2α zatem |∡ADC|=α. Więc
powstał kolejny trójkąt równoramienny na podstawie kątów, ale jedno ramię równe jest 4, a
drugie 6 więc gdzieś popełniłem błąd. Chciałbym zrozumieć co jest złego w moim rozumowaniu 