Prawdopodobieństwo klasyczne Patryk: Rzucamy kostką do gry. Jeśli wypadła nam parzysta liczba oczek, rzucamy monetą. Jeśli wypadła nam nieparzysta liczba oczek, rzucamy jeszcze raz kostką. Opisz przestrzeń wszystkich zdarzeń elementarnych. Wyznacz zbiór zdarzeń sprzyjających zdarzeniu, że w całym doświadczeniu wyrzucimy chociaż raz parzystą liczbę oczek i oblicz jego prawdopodobieństwo. Udało mi się obliczyć ,że Ω = 15 to są wszystkie możliwości.Teraz nie wiem skąd wzieli ,aż 19 zbiórów zdarzeń sprzyjających zdarzeniu. Wynik wynosi 285. Może mi ktoś wyjaśnić ten zbiór A (19)? Z góry dziękuję

Patryk: Już rozwiązałem

wmboczek: 6 zdarzeń koska−moneta 18 zdarzeń kostka−kostka P=(6+9)/24 Na pewno treść dobra?

Patryk: Treść dobra tylko na złą odpowiedź spojrzałem (głupek)

wmboczek: Przy czym z drzewka wychodzi P=0.75 bo zdarzenia nie są równoprawdopodobne

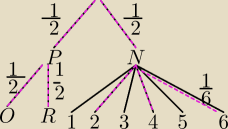
Mila: A−Wyrzucono choć raz parzystą liczbę oczek A={(2,0),(2,R) , (4,O),(4,R),(6,O),(6,R),(1,2),(1,4),(1,6),(3,2),(3,4),(3,6),(5,2),(5,4),(5,6)} |A|=15 Zdarzenia nie są jednakowo prawdopodobne. Liczę P(A) z drzewka>

	1		1		1		1		1		1
P(A)=		*		+		*		+3*		*		=
	2		2		2		2		2		6

	1		1		3
=		+		=
	2		4		4

Mila: Ω={(1,1),(1,2),(1,3), (1,4),(1,5),(1,6),(2,O),(2,R), wypisuj dalej sam

Patryk: Dziękuję za rozwiązania ,ale tak jak wcześniej napisałem już udało mi się dojść do poprawnej odpowiedźi samemu