Ciągłość funkcji
Ciąg: Wyznacz takie parametry a,b
| | ⎧ | ax+5 dla |x|>2 | |
| f(x) = | ⎩ | (x−b)2 dla |x|≤2 |
|
by funkcja była ciągła na całej prostej rzeczywistej.
Rozumiem, że nie powinienem martwić się o ciągłość funkcji liniowej i wielomianowej w danych
przedziałach, jak jednak zająć się granicami w punktach sklejenia? Moglibyście wyjaśnić?
22 sty 20:34
Szkolniak: | | ⎧ | ax+5, gdy |x|>2 | |
| f(x)= | ⎩ | (x−b)2, gdy |x|≤2 |
|
f(−2)=−2a+5
f(−2)=(−2−b)
2
obie wartości muszą być równe, aby funkcja była w tym punkcie ciągła, więc −2a+5=(b+2)
2
f(2)=2a+5
f(2)=(2−b)
2
obie wartości muszą być równe.. , więc 2a+5=(b−2)
2
| ⎧ | −2a+5=b2+4b+4 | |
| ⎩ | 2a+5=b2−4b+4 |
|
10=2b
2+8 ⇔ b
2=1 ⇔ b∊{−1,1}
1
o b=−1 ⇒ a=2
v2
8 b=1 ⇒ a=−2
zatem: (a=2 ∧ b=−1) v (a=−2 ∧ b=1)
22 sty 22:18
Mila:
f(2)=(2−b)
2
lim
x→2+(ax+5)=(2−b)
2
f(−2)=(−2−b)
2
lim
x→−2−(ax+5)=(−2−b)
2
(2a+5)=(2−b)
2
−2a+5=(2+b)
2
=========== +
10=2b
2+8
b=1 lub b=−1
1) dla b=1 a=−2
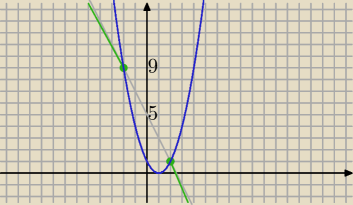
f(x)=−2x+5 dla x>2 lub x<−2
lub
f(x)=(x−1)
2 dla x∊<−2,2>
licz dalej i sprawdzaj granice w x=−2 i x=2
2) dla b=−1
a=2
22 sty 22:25
 f(2)=(2−b)2
limx→2+(ax+5)=(2−b)2
f(−2)=(−2−b)2
limx→−2−(ax+5)=(−2−b)2
(2a+5)=(2−b)2
−2a+5=(2+b)2
=========== +
10=2b2+8
b=1 lub b=−1
1) dla b=1 a=−2
f(x)=−2x+5 dla x>2 lub x<−2
lub
f(x)=(x−1)2 dla x∊<−2,2>
licz dalej i sprawdzaj granice w x=−2 i x=2
2) dla b=−1
a=2
f(2)=(2−b)2
limx→2+(ax+5)=(2−b)2
f(−2)=(−2−b)2
limx→−2−(ax+5)=(−2−b)2
(2a+5)=(2−b)2
−2a+5=(2+b)2
=========== +
10=2b2+8
b=1 lub b=−1
1) dla b=1 a=−2
f(x)=−2x+5 dla x>2 lub x<−2
lub
f(x)=(x−1)2 dla x∊<−2,2>
licz dalej i sprawdzaj granice w x=−2 i x=2
2) dla b=−1
a=2