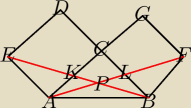
Dowod T: Na przyprostokątnych AC i BC trojkata prostokątnego ABC zbudowano, na zewnątrz trojkata kwadraty ACDE i BFGC. Odcinek AF przecina przyprostokątną BC w punkcie L, a odcinek BE przecina przyprostokatna AC w punkcie K

KP		LP
	=		→ KP * PB = LP * AP → BK = AL, czyli odcinek KC = LC ⇔ gdy AC = BC?
AP		PB

Da się jakość wykazać AC = BC? Dobry sposób myślenia?

a7: Czy może chodzi o to zadanie? https://zadania.info/d144/5321763

T: Tak, tylk zastanawiam się czy moim sposobem dałoby się to jakoś udowodnić, tzn czy dałoby się udowodnić ze ac = BC?

Mila: Podaj polecenie do zadania. Czy masz w treści podane, że prostokątny ΔABC jest równoramienny , czy dowolny dowolny.

a7: ale w zadaniu z 20:27 AC niekoniecznie równa się BC, jedynie jest wykazane, że KC=LC, a to nie to samo

T: Polecenie to udowodnij iż KC = LC

T: Tak, stad moje pytanie czy da się jakoś wykazać ze AC = BC

a7: AC i BC mogą być dowolnymi przyprostokątnymi

T: Mamy dwa trójkąty prostokątne ALC i BCK skoro BK = AL to KC = AC ⇔ AC = BC

T: ktoś cos?

Mila:

	KC		ED
ΔKCB∼ΔEDB⇔		=		⇔
	CB		DB

KC		b		ab
	=		⇔|KC|=
a		a+b		a+b

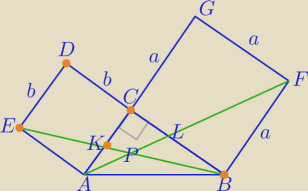
ΔACL∼AGF⇔

CL		GF		CL
	=		⇔		{a}{a+b}
AC		GA		b

	ab
|CL|=		⇔
	a+b

|KC|=|CL| ========

	ab
|BK|2=(		)2+a2
	a+b

	ab
|AL|2=(		)2+b2
	a+b

|BK²=|AL|² tylko wtedy gdy a=b czyli dla prostokątnego równoramiennego ΔABC !

T: Dzięki!