Logarytmy Daniel: Witam mam problem z zadaniem. Dla jakich argumentów wyrażenie log_3/2 (2x−4x²) przyjmuje wartości niedodatnie

Jerzy: Dla 2x − 4x² ≤ 1

Daniel: Czemu 1? Właśnie nie rozumiem jak to zbudować bo mniejsze wieksze rozumien, bo nie dodatnie

Mila: 1) D: 2x−4x²>0 2x*(1−2x)>0

	1
x∊(0,		)
	2

	1
log3/2 (2x−4x2)≤0 i x∊(0,		) ⇔
	2

	1
log3/2 (2x−4x2)≤log3/2(1 ) i x∊(0,		)
	2

	1
0<2x−4x2≤1 i x∊(0,		)
	2

	3
[dla		>1
	2

[ funkcja log_3/2 (x) przyjmuje wartości ≤0 dla argumentów z przedziału (0,1> ] 2x−4x²≤1⇔ 4x²−2x+1≥0 Δ<0⇔4x²−2x+1>0 dla x∊R

	1
⇔log3/2 (2x−4x2)≤0 dla x∊(0,		)
	2

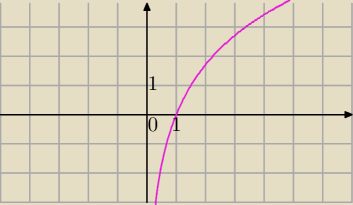
Jerzy: Funkcja f(x) = log_ax , dla a > 1 przyjmuje wrtości niedodatnie gdy liczba logarytmowana x ≤ 1. Popatrz na wykres funkcji logarytmicznej dla a ∊ (0,1) oraz dla a > 1