Może ktoś ma ochotę to rozwiązać Michael: Znajdź równanie płaszczyzny zawierającej punkt p (1,0,2) oraz prostą : x=t , y=t+1 , z=t+2

Blee: 1) wyznaczasz dowolny punkt na prostej 2) wyznaczasz wektor zaczepiony w tymże punkcie który 'leży na' prostej 3) wyznaczasz wektor zaczepiony w tymże punkcie, w kierunku punktu p 4) iloczyn wektorowy tych wektorów daje Ci wektor normalny szukanej płaszczyzny 5) piszesz wzór płaszczyzny (mając jego wektor normalny)

Michael: 3) wyznaczasz wektor zaczepiony w tymże punkcie, w kierunku punktu p jak to zrobić? myślałem żeby wyznaczyć 2 punkty na prostej i utworzyć wektory 2 wektory przechodzące przez te punkty i zn nich wyliczyć wektor normalny

Michael: ale nie jestem pewny tego wyznaczania punktu, można podstawić dowolną liczbę rzeczywistą pod t i z tego wyliczyc 2 punkty np t=1, t=2

Bleee: Wyznacz wektor z punktu A (ten na prostej) do punktu P. Masz współrzędne punktów. Wyznaczanie wektorów miałeś w szkole średniej (albo gimnazjum)

Bleee: Tak. Podstawiaj jakieś t, np. t = 1

Michael: czyli AP X V ?

Blee: tak

Jerzy: Tak,ten iloczyn to wektor normalny szukanej płaszczyzny. @Blee,18:17 , po co punkt 2) ?

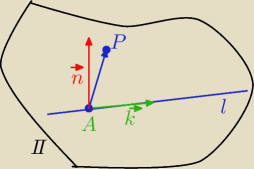
Mila: P= (1,0,2) prosta l: x=t y=1+t z=2+t A=(0,1,2)∊l k^→=[1,1,1] − wektor kierunkowy prostej AP^→=[1,−1,0] n^→=[1,1,1] x [1,−1,0] =[1,1,−2]− wektor normalny szukanej płaszczyzny π: 1*(x−1)+1*(y−0)−2*(z−2)=0 π: x+y−2z+3=0 ============