funkcja analiza: Funkcja ciagła f : R→R jest dwukrotnie rózniczkowalna w zbiorze R\{0}, przy czym f''(x)=1 dla kazdej liczby rzeczywistej x≠0. Ponadto wiadomo, ze f(−3)=−3, f(−1)=−1, f(1)=1 . Wyznaczyc f(5).

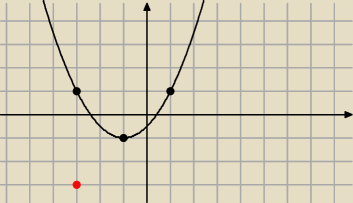
Blee: na pewno TAKIE są wartości funkcji

analiza: Tak

Blee: skoro f''(x) = 1 dla każdego x∊ R/{0} to znaczy że f'(x) = x dla każdego x∊ R/{0} a to znaczy, że funkcja f(x) jest malejąca w przedziale (−∞; 0) co jest sprzeczne z danymi zadania

analiza: Tresc zadania jest dobrze.

ABC: Blee o północy zaczyna mówić nieprawdziwe rzeczy , f''(x)=1 to f'(x)=x+c

Blee: ABC masz rację, co nie zmienia faktu, że dane nie pasują. f'(x) = x+a

	1
f(x) =		(x+a)2 + b
	2

	(1+a)2 − (1−a)2		4a
f(1) − f(−1) =		=		= 2 −> a = 1
	2		2

czyli funkcja jest malejąca na przedziale (−3;−1) co się nie zgadza z danymi.