Oblicz obwód trójkąta ABC Koło: Cześć. Potrzebuje pomocy z tym zadaniem.Chodzi mi o podpunkt C Dany jest trójkąt prostokątny ABC, o kącie prostym przy wierzchołku C. Punkt D jest spodkiem wysokości CD. Pola trójkątów ABC i ACD różnią się o 42. Pole trójkąta BCD stanowi 75% pola trójkąta ACD. a) Oblicz skalę podobieństwa trójkątów BCD i ACD. b) Podaj, z dokładnością do , miary kątów ostrych trójkąta ABC. c) Oblicz obwód trójkąta ABC.

Koło: Podpunkt A i B zrobiłem,ale mam problem z podpunktem C

a@b: Jaką masz odp: do c)

Koło:

	2+√3+√7
Powinno być √392√3*		pod pierwiastkiem jest 392 przez √3
	2

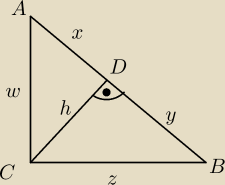
Blee: oznaczmy: Δ_ABC = Δ1 Δ_ACD = Δ2 Δ_BCD = Δ3 PΔ1 = PΔ2 + 42 −> PΔ3 = 42 PΔ3 = 75%*PΔ2 −> PΔ2 = 56 więc PΔ1 = 98 i teraz równania:

1
	w*z = 98
2

1
	xh = 56
2

1
	yh = 42
2

w² = h² + x² z² = h² + y² ale też można inaczej:

1
	xh = 56
2

1
	yh = 42
2

	4
z tego wynika, że: x =		y
	3

Δ2 i Δ3 są podobne, więc:

y		h		4		2√3
	=		−> h2 = yx =		y2 −> h =		y
h		x		3		3

	y*h		1		2√3		√3
tak więc: PΔ3 =		=		*y*		y =		y2 −> y =
	2		2		3		3

−> x = Wyznaczoną proporcję boków stosujemy do Δ1 cele wyznaczenia boków w i z Obliczamy obwód

Koło: Dziękuję za pomoc

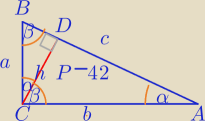
Mila: 1)

	√3
ΔBCD∼ΔACD w skali k=
	2

stąd:

	√3
a=		b
	2

======== z tw. Pitagorasa: c²=a²+b²

	√3
c2=(		b)2+b2
	2

	√7
c=		b
	2

========== 2)

	c		√7   b 2
ΔABC∼ΔCDA w skali k=		=
	b		b

	PΔABC		7
⇔		=
	PCDA		4

Pola trójkątów ABC i ACD różnią się o 42⇔ P_ΔABC=P

P		7
	=
[ACD]		4

4P=7*(P−42) P=98

	1
P=		a*b
	2

	1		√3
98=		*		b*b
	2		2

========]============= Oblicz a, b i c Eta masz inny sposób ?

a@b: Hej Mila Mam tak samo......

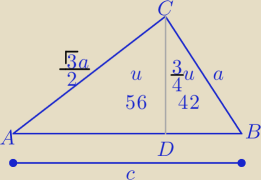
a@b: P(ABC)=98

	42		√3
k2=		⇒ k=
	56		2

	√7
c=
	2

	a
Obwód L=		(√3+√7+2)
	2

	1		√3
i z pola 98=		*a*
	2		2

a=.............

a@b:

	1		√3
98=		*a*		*a
	2		2

Mila: Witaj! Właśnie te pierwiastki chciałam ominąć, ale widać tak musi być Dziękuję za odpowiedź.

a@b: