W sześcianie ABCDA'B'C'D' o krawędzi długości 120 punkt P jest środkiem krawędzi Klaudia: W sześcianie ABCDA'B'C'D' o krawędzi długości 120 punkt P jest środkiem krawędzi AA', punkt Q środkiem krawędzi BC, zaś punkt R środkiem przekątnej górnej podstawy. Oblicz cos kąta PQR i pole powierzchni trójkąta PQR

Saizou :

	1		4a√2
|A'R|=		•		=a√2
	2		2

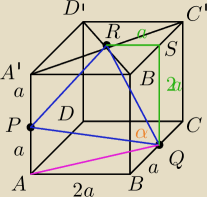
PQ, QR, PR z Pitagorasa cosα → tw. cosinusów

	1
P=		•|PQ|•|QR|•sinα
	2

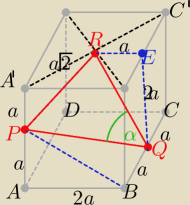
a@b: Wprowadź oznaczenia 2a=120 Policz kwadraty długości boków z tw. Pitagorasa odpowiednio w trójkątach ABP, QRE, PRA^' i BPQ Następnie z tw. cosinusów w ΔPQR wyznacz cosα oraz

	1
P(PQR)=		*|PQ|*|RQ|*sinα , sinα=√1−cos2α
	2

.................. dokończ

a@b:

Klaudia: średnio mi wychodzi wyznaczenie cosα, według obliczeń wyszedł mi −0,0698212

Klaudia: a dobra mój błąd, dobrze wyszło wszystko, dziekuje

a@b: