Czy ta funkcja ma w ogóle jakieś ekstremum? Proszę o pomoc Baryłka: Wyznacz przedziały monotoniczności oraz ekstrema lokalne funkcji f o równaniu: 9x−1/x²

salamandra:

9x−1
	?
x2

Malami:

a@b:

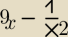
	1
f(x)= 9x−		,x≠0
	x2

	2
f'(x)= 9+
	x3

f^'(x)=0 ⇒......

Baryłka: Czyli x = −√(2/9)?

salamandra: Liczysz pochodną ilorazu:

	9*x2−(9x−1)2x		9x2−18x2+2x		−9x2+2x		x(−9x+2)
f'(x) =		=		=		=		=
	x4		x4		x4		x4

	−9x+2
=
	x3

	2
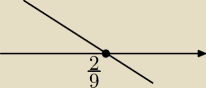
f'(x) = 0 ⇔ −9x+2 = 0 ⇔ −9x = −2 ⇔ x =
	9

	2		2
Funkcja jest rosnąca w przedziale (−∞;		), a malejąca w przedziale (		; ∞)
	9		9

	2
Funkcja osiąga maximum lokalne w punkcie
	9

	2
czyli ymax = f(		) = 20,25
	9

Malami: A skąd 2/x³ ?

salamandra: No, czyli jednak nie to... w każdym razie na tej samej zasadzie

salamandra:

	9x−1
Ja liczyłem dla		, żebyś nie myślał, że to do Twojego.
	x2

a@b:

	1		1		2
(		)'= −		*2x = −
	x2		x4		x3

salamandra: [f(x)−g(x)]' = f'(x)−g'(x) f(x)= 9x, więc f'(x) = 9

	1		2x		2
g(x) =		, więc na g'(x) stosujemy pochodną ilorazu		=
	x2		x4		x3

a@b: zgubiłeś minus

salamandra: minus zgubiłem oczywiście, bo

f'(x)*g(x)−f(x)*g'(x)		0*x2−1*2x		−2x		−2
	=		=		=
(g(x))2		x4		x4		x3

a@b: