Nowe zadanka
Saizou :
Tym razem na warsztat weźmiemy .... geometrię
Zad 1
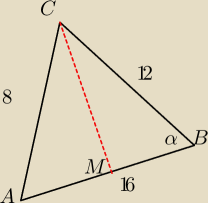
Boki trójkąa mają długości 8, 12 i 16. Oblicz długość środkowej poprowadzonej do najdłuższego
boku.
Zad 2
Długości boków trójkąta są kolejnymi liczbami naturalnymi.
Kąty wewnętrzne tego trójkąta mają tę własność, że miara kąta największego
jest dwukrotnością miary kąta najmnieszego. Oblicz długości boków tego trójkąta.
Zad 3
Bok pięciokąta formenego ma długość a. Wykaż, że każda przekątna tego pięciokąta
| | a(1+√5 | |
ma długość równą |
| |
| | 2 | |
Zad 4
Kąt ostry równoległoboku ma miarę 60°, a jego dłuższa przekątna ma długość równą 3
√7.
Wiedząc, że rówżnica długości jego boków jest równa 3, oblicz pole tego równoległoboku
i długość jego krótszej przekątnej.
Zad 5
Pole trójkąa ABC jest równe 40
√3, kąt CAB ma miarę 60°, a suma długości boków AB i AC
jest równa 26. Oblicz odległość d środka O okręgu opisanego na tym trójkącie od boku BC.
17 sty 14:25
salamandra: Zad 2 miałem wczoraj na lekcji

17 sty 14:58
Saizou :
Zadania pochodzą ze zbioru wydawnictwa Podkowa
17 sty 15:00
salamandra:
Dokładnie z tego wydawnictwa książkę realizuję

.
Ok, trzeba coś zrobić
Zad 1.
tw. cosinusów:
8
2= 12
2+16
2−2*12*16*cosα
64=144+256−384*cosα
−336=−384*cosα
α≈29 stopni
|CM|
2 = 8
2+12
2−2*8*12*cos29
|CM|
2 = 64+144−192*cos29
|CM|
2 = 208−192*0,875
|CM|
2 = 208−168 = 40
|CM| =
√40
Dobrze?
17 sty 15:11
Saizou :
Nie możesz przybliżać wartości kąta α. Ale metoda dobra.
17 sty 15:16
salamandra: Nie jestem w stanie wyznaczyć dokładnie ile on wynosi, bo cosα = 0,875
17 sty 15:17
salamandra: W zasadzie ten kąt mi jest do niczego niepotrzebny, bo jak widzisz, pod "cos29" wstawiłem
jednak tę dokładną wartość.
17 sty 15:18
Saizou :
| | 336 | |
Czyli musisz zostawić, że cosα= |
| i tego używać później. |
| | 384 | |
17 sty 15:19
salamandra: Wynik dobry?
17 sty 15:20
Saizou : | | −366 | | 7 | |
Wynik jest okej, bo cosα= |
| = |
| =0,875 |
| | 384 | | 8 | |
17 sty 15:23
Saizou :
Przybliżeń używamy tylko wtedy, gdy chcą to w zadaniu, poza tym liczymy z dokładnymi
wartościami
17 sty 15:24
salamandra:
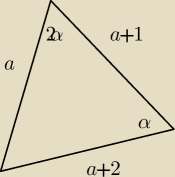
Zad 2.
| a+2 | | a | |
| = |
| / *sinα |
| 2sinαcosα | | sinα | |
a+2=2cosα*a/ :a
a
2=(a+2)
2+(a+1)
2−2(a+1)(a+2)*cosα
a
2=a
2+4a+4+a
2+2a+1−2(a
2+2a+a+2)*cosα
a
2=2a
2+6a+5−2(a
2+3a+2)*cosα
a
2=2a
2+6a+5−(2a
2+6a+4)*cosα
| | a+2 | |
a2=2a2+6a+5−(2a2+6a+4)* |
| |
| | 2a | |
| | 2a3+4a2 | | 6a2+12a | | 4a+8 | |
a2=2a2+6a+5−( |
| + |
| + |
| ) |
| | 2a | | 2a | | 2a | |
| | 8 | |
a2=2a2+6a+5−(a2+2a+3a+6+2+ |
| ) |
| | 2a | |
| | 2a2−6a−8 | |
0= |
| ⇔ 2a2−6a−8 = 0 |
| | 2a | |
2a
2−6a−8=0
Δ=36+64= 100
Odp. Boki tego trójkąta to 4,5,6
17 sty 15:38
a@b:
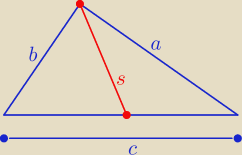
zad1/
długość środkowej s wyraża się wzorem:
| | 1 | |
s= |
| √2a2+2b2−c2 , gdzie c −− najdłuższy bok |
| | 2 | |
s=2
√10
=======
ten wzór możesz sobie wyprowadzić z tw.cosinusów w tym trójkącie
17 sty 15:41
Saizou : 
Przy równaniu kwadratowym mogłeś podzielić przez 2, byłby mniejsze liczby
17 sty 15:53
a@b:

zad 2/
Takie wprowadzenie oznaczeń boków znacznie ułatwia obliczenia
oraz z tw. cosinusów: ( po przekształceniu wzorów :
i mamy
| | n−1 | | n+1 | |
z tw. sinusów |
| = |
| , cos2α=2sinαcosα, sinα≠0 |
| | sinα | | cos2α | |
| | n2+(n+1)2−(n−1)2 | | n+4 | |
i cosα= |
| ⇒ cosα= |
| |
| | 2n(n+1) | | 2(n+1) | |
| | n+1 | | n+4 | |
zatem: |
| = |
| ⇒ ..... n=5 |
| | 2(n−1) | | 2(n+1) | |
To boki mają długość
4,5,6
========
17 sty 16:07
Szkolniak:

a+b=26 ⇒ a=26−b
P=40
√3
| | √3 | |
zatem: 80√3=ab* |
| ⇒ ab=160 |
| | 2 | |
b(26−b)=160
−b
2+26b−160=0
b
2−26b+160=0
(b−10)(b−16)=0
b=10 v b=16
b∊{10,16}
1
o b=10 ⇒ a=16
v2
o b=16 ⇒ a=10
z twierdzenia cosinusów dla c:
c
2=100+256−160
c
2=196 ⇒ c=14
z twierdzenia sinusów:
okrąg zbudowany na symetralnych boków, więc:
| | c | |
( |
| )2+g2=R2, gdzie g to szukana odległość |
| | 2 | |
17 sty 19:50
Saizou :
Ładnie, chociaż brakuje komentarza dlaczego rozważamy tylko jedną wersję boków a i b.
Nieścisłe jest sformułowanie "okrąg zbudowany na symetralnych boków"
17 sty 20:16
Saizou :
Zachęcam do dalszego rozwiązywania

Jutro pojawią się zadanka z kombinatoryki i prawdopodobieństwa
17 sty 22:06
salamandra: Podejmę się jutro, no a kombinatoryki i prawdopodobieństwa nie tknę, bo jeszcze tego nie miałem

17 sty 22:36
Saizou :
To może geometria analityczna?
17 sty 23:00
salamandra: Może być, trzeba szlifować to z czego się jest słabszym

17 sty 23:22
a@b:

17 sty 23:23
Saizou : Najpierw trzeba skończyć zadania z tego postu.
Eta może coś wrzucisz dla naszych rodzynków?
17 sty 23:56
Saizou :
Zostały zadanie 3 i 4
18 sty 11:02
Saizou : Podbijam dla chętnych maturzystów
18 sty 20:41
a@b:
Hej
Saizou 
Maturzyści
balują na studniówce

18 sty 21:10
Saizou : Tydzień temu też balowali

18 sty 21:12
a@b:
Ja też za tydzień

18 sty 21:31
Saizou :
W sumie to, która matura z rzędu? ^^
18 sty 21:36
a@b:
"grono" .... baluje co rok ( nawet na trzech i czterech .....

18 sty 21:38
Saizou :
Udanej zabawy

18 sty 21:39
a@b:
dzięki

18 sty 21:44
a@b:
zad5 dla maturzystów

W ΔABC w którym |∡BAC|=135
o i |AC|=b
poprowadzono środkową AD, która jest prostopadła do boku AC
Wykaż,że |AB|=b
√2
18 sty 23:45
Patryk: Czy to zadanie jest dobrze skonstruowane? Bo wychodzi mi z rysunku trójkąt ABD który ma kąty
135 i 90 ... chyba że ja źle narysowałem
18 sty 23:51
a@b:
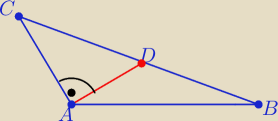
19 sty 00:20
jc: Dodam swoje zadanie.
Trójkąt równoboczny ABC jest wpisany w okrąg. Na (krótszym) łuku okręgu AB leży punkt P.
Pokazać, że AP + BP = CP.
19 sty 00:47
Saizou :
Eta 2 razy tw. sinusów i jak to mówisz "po potokach"
19 sty 13:00
a@b:
Hej
Saizou 
Jeżeli mówisz o zad 5/ to jeszcze prościej ( jednym równaniem

19 sty 13:07
Saizou :
To będę myśleć
 jc
jc 3 razy tw. sinusów + info że promień okręgu opisanego na trójkątach jest jednakowy.
19 sty 13:11
a@b:
W zad
jc
Tw. Ptolemeusza ... i po ptokach

19 sty 13:12
Saizou :
W sumie jest coś takiego

19 sty 13:15
a@b:

2 sposób ( zad jc) ....... 2 razy tw. cosinusów
19 sty 13:17
jc:
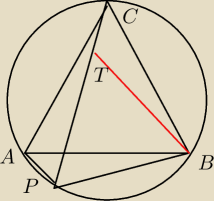
Faktycznie, Ptolemeusz daje od razu wynik.
Ja zobaczyłem rzecz na rysunku. T stawiamy tak, aby PT=PB. Wtedy TC=AP
(trójkąt BAP powstaje z trójkąta BCT przez obrót względem B o 60 stopni).
19 sty 13:35
a@b:
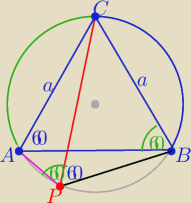
1/ 2 razy z tw. cosinusów
|AP|
2+|PC|
2−|AP|*|PC|=a
2
|BP|
2+|PC|
2−|BP|*|PC|=a
2
.........................
i mamy tezę
19 sty 13:52
Szkolniak: 4) Czy w równoległoboku przekątne zawsze dzielą kąt na pół?
19 sty 15:44
a@b:

I jak myślisz?

19 sty 19:04
a@b:
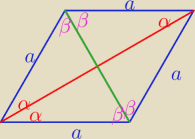
tylko w rombie i kwadracie
19 sty 19:07
salamandra: Zad 4.
Przekątna 3√7 będzie przecinała kąt 60 stopni czy 120?
19 sty 20:11
salamandra: Boki 3 i 6, a przekątna druga 3√3 czy źle?
19 sty 20:34
a@b:
Dobrze

19 sty 20:50
salamandra: Piszę z telefonu. dlatego nie chciałem pisać rozwiązania niemając pewności, że jest dobrze. W
takim razie:
Boki: a, a+3
Tw. Cosinusów:
(3
√7)
2= a
2+(a+3)
2−2a(a+3)*cos120
| | 1 | |
63= a2+a2+6a+9−(2a2+6a)+(− |
| ) |
| | 2 | |
3a
2+9a−54=0
a
2+3a−18=0
Δ=81
a1<0
a2=3
Boki: 3,6
Znów tw cosinusów:
f − krótsza przekątna
f
2= 36+9−2*3*6*cos60
f=
√27=3
√3
| | 1 | | √3 | | 18√3 | |
P=2*( |
| *3*6*sin120)=2*(9* |
| )= |
| =9√3 |
| | 2 | | 2 | | 2 | |
19 sty 20:57
a@b:

Przez f −− zwykle oznaczamy dłuższą ( bo litera f dłuższa od e

19 sty 21:15
Szkolniak: Skubany

Ale widzę że większość zadań idzie z tych twierdzeń cosinusów/sinusów
19 sty 21:20
salamandra: Ok

, poza tym dobrze?
19 sty 21:20
salamandra: Tez to zauważyłem. Dopóki tych twierdzeń nie znałem, większość takich zadań to czarna magia, a
dzięki im, nagle się horyzonty rozszerzają
19 sty 21:23
salamandra: nim*
19 sty 21:23
Szkolniak: To prawda, przedtem też ich nie znałem, a teraz robiąc zadania to wystarczy gdziekolwiek
jednego z twierdzeń użyć i nagle po zadaniu

19 sty 21:25
Saizou :
Zadania były tak dobrane aby używać tw, cosinusów i sinusów

Pozostało zadanie z pięciokątem. Jak je rozwiążecie wrzucę analityczną
20 sty 10:24
Szkolniak:

W jaki sposób teraz dojść jakie kąty są przy poszczególnych wierzchołkach? Czy nie jest mi to
tutaj potrzebne?
20 sty 15:14
Saizou :
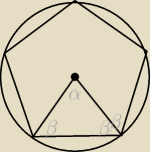
Jeśli chcesz tak liczyć, to
... β=36 ⇒2β=72
Pojawi się problem cos72
Inna prostsza metoda to podobieństwo trójkątów
20 sty 15:29
Mila:
Podpowiedź.
1) suma kątów : 3*180
o=540
o
kąty wewnętrzne 5−kąta mają po 108
o.
2) Masz tam trójkąty równoramienne, łatwo obliczysz kąty.
Znajdź trójkąty podobne , będziesz miał złotą proporcję i to będzie koniec !
20 sty 15:32
Szkolniak: Na tym moim rysunku widoczne są te trójkąty podobne?
Bo coś nie mogę tego zauważyć
20 sty 20:48
Mila:
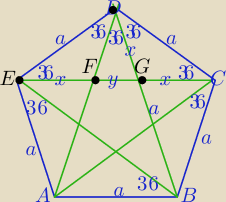
1) ΔACB≡ΔBDC≡ΔECD≡ΔDAE≡ΔEBA cecha bkb
p− długość każdej przekątnej
2) ΔGDE∼ΔEDB⇔
|GB|=a
p*(p−a)=a
2
p
2−ap−a
2=0, a>0, p>0
Δ=a
2+4a
2=5a
2
| | a−a√5 | | a+a√5 | |
p= |
| <0 lub p= |
| |
| | 2 | | 2 | |
=============
20 sty 20:50
Saizou :
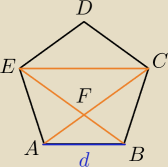
1° uzasadnij, że |CF|=|EF|=a (pokaż, że czworokąt EFCD jest rombem)
2° uzasadnij, że ΔCDE ~ Δ BFA
3° wykaż to, o co proszą w zadaniu

20 sty 20:54
Szkolniak: Fajne zadanie, nie wpadłbym na to

20 sty 21:36
Mila:
Zauważyłeś trójkąty podobne?
20 sty 21:45
wmboczek: Jest jeszcze opcja z równaniem trygonometrycznym
p/a=2cos36=a/x
i rozpisanie tw cosinusów dla EFD ze wzorem na cos3α
20 sty 22:13

 Dokładnie z tego wydawnictwa książkę realizuję
Dokładnie z tego wydawnictwa książkę realizuję  .
Ok, trzeba coś zrobić
Zad 1.
tw. cosinusów:
82= 122+162−2*12*16*cosα
64=144+256−384*cosα
−336=−384*cosα
.
Ok, trzeba coś zrobić
Zad 1.
tw. cosinusów:
82= 122+162−2*12*16*cosα
64=144+256−384*cosα
−336=−384*cosα
 Zad 2.
Zad 2.
 zad1/
długość środkowej s wyraża się wzorem:
zad1/
długość środkowej s wyraża się wzorem:
 Przy równaniu kwadratowym mogłeś podzielić przez 2, byłby mniejsze liczby
Przy równaniu kwadratowym mogłeś podzielić przez 2, byłby mniejsze liczby
 zad 2/
Takie wprowadzenie oznaczeń boków znacznie ułatwia obliczenia
oraz z tw. cosinusów: ( po przekształceniu wzorów :
zad 2/
Takie wprowadzenie oznaczeń boków znacznie ułatwia obliczenia
oraz z tw. cosinusów: ( po przekształceniu wzorów :
 a+b=26 ⇒ a=26−b
P=40√3
a+b=26 ⇒ a=26−b
P=40√3
 Jutro pojawią się zadanka z kombinatoryki i prawdopodobieństwa
Jutro pojawią się zadanka z kombinatoryki i prawdopodobieństwa



 Maturzyści balują na studniówce
Maturzyści balują na studniówce 





 W ΔABC w którym |∡BAC|=135o i |AC|=b
poprowadzono środkową AD, która jest prostopadła do boku AC
Wykaż,że |AB|=b√2
W ΔABC w którym |∡BAC|=135o i |AC|=b
poprowadzono środkową AD, która jest prostopadła do boku AC
Wykaż,że |AB|=b√2

 Jeżeli mówisz o zad 5/ to jeszcze prościej ( jednym równaniem
Jeżeli mówisz o zad 5/ to jeszcze prościej ( jednym równaniem 
 jc 3 razy tw. sinusów + info że promień okręgu opisanego na trójkątach jest jednakowy.
jc 3 razy tw. sinusów + info że promień okręgu opisanego na trójkątach jest jednakowy.


 2 sposób ( zad jc) ....... 2 razy tw. cosinusów
2 sposób ( zad jc) ....... 2 razy tw. cosinusów
 Faktycznie, Ptolemeusz daje od razu wynik.
Ja zobaczyłem rzecz na rysunku. T stawiamy tak, aby PT=PB. Wtedy TC=AP
(trójkąt BAP powstaje z trójkąta BCT przez obrót względem B o 60 stopni).
Faktycznie, Ptolemeusz daje od razu wynik.
Ja zobaczyłem rzecz na rysunku. T stawiamy tak, aby PT=PB. Wtedy TC=AP
(trójkąt BAP powstaje z trójkąta BCT przez obrót względem B o 60 stopni).
 1/ 2 razy z tw. cosinusów
|AP|2+|PC|2−|AP|*|PC|=a2
|BP|2+|PC|2−|BP|*|PC|=a2
.........................
i mamy tezę
1/ 2 razy z tw. cosinusów
|AP|2+|PC|2−|AP|*|PC|=a2
|BP|2+|PC|2−|BP|*|PC|=a2
.........................
i mamy tezę
 I jak myślisz?
I jak myślisz?

 tylko w rombie i kwadracie
tylko w rombie i kwadracie

 Przez f −− zwykle oznaczamy dłuższą ( bo litera f dłuższa od e
Przez f −− zwykle oznaczamy dłuższą ( bo litera f dłuższa od e

 Ale widzę że większość zadań idzie z tych twierdzeń cosinusów/sinusów
Ale widzę że większość zadań idzie z tych twierdzeń cosinusów/sinusów
 , poza tym dobrze?
, poza tym dobrze?

 Pozostało zadanie z pięciokątem. Jak je rozwiążecie wrzucę analityczną
Pozostało zadanie z pięciokątem. Jak je rozwiążecie wrzucę analityczną
 W jaki sposób teraz dojść jakie kąty są przy poszczególnych wierzchołkach? Czy nie jest mi to
tutaj potrzebne?
W jaki sposób teraz dojść jakie kąty są przy poszczególnych wierzchołkach? Czy nie jest mi to
tutaj potrzebne?
 Jeśli chcesz tak liczyć, to
Jeśli chcesz tak liczyć, to
 1) ΔACB≡ΔBDC≡ΔECD≡ΔDAE≡ΔEBA cecha bkb
p− długość każdej przekątnej
2) ΔGDE∼ΔEDB⇔
|GB|=a
1) ΔACB≡ΔBDC≡ΔECD≡ΔDAE≡ΔEBA cecha bkb
p− długość każdej przekątnej
2) ΔGDE∼ΔEDB⇔
|GB|=a
 1° uzasadnij, że |CF|=|EF|=a (pokaż, że czworokąt EFCD jest rombem)
2° uzasadnij, że ΔCDE ~ Δ BFA
3° wykaż to, o co proszą w zadaniu
1° uzasadnij, że |CF|=|EF|=a (pokaż, że czworokąt EFCD jest rombem)
2° uzasadnij, że ΔCDE ~ Δ BFA
3° wykaż to, o co proszą w zadaniu 
