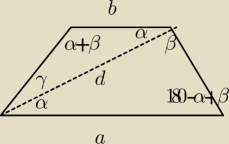
twierdzenie sinusów salamandra: W trapezie równoramiennym przekątna ma długość d i tworzy z dłuższą podstawą kąt α, a z ramieniem kąt β. Oblicz dlugosci podstaw tego trapezu Tam na rysunku gdzie 180−(α+β) powinien być ten nawias, niestety nie mogłem go dodać na rysunku sin(180−(α+β)) = sin(α+β)

d		a
	=
sin(α+β)		sinβ

a*sin(α+β) = d*sinβ

	d*sinβ
a =
	sin(α+β)

γ= 180−(2α+β) sinγ = sin(2α+β)

b		d
	=
sin(2α+β)		sin(α+β)

b*sin(α+β) = d*sin(2α+β)

	d*sin(2α+β)
b=
	sin(α+β)

I to tyle? bo nie wiem co autor zadania miał na myśli. I z góry mam pytanie, jako, że tylko rysunek miałem w podpowiedzi − dlaczego tam gdzie γ, nie jest β jako kąt naprzemianległy, tak jak w przypadku α?

Saizou :

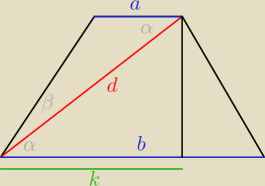
	a+b
k=
	2

	k
cosα=
	d

k=dcosα a+b=2dcosα Z tw. sinusów

a		d
	=
sinβ		sin(180−(α+β))

a		d
	=
sinβ		sin(α+β)

asin(α+β)=dsinβ

	dsinβ
a=
	sin(α+β)

	dsinβ
b=2dcosα−
	sin(α+β)

a@b:

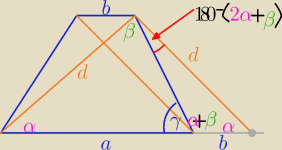
a		d		dsinβ
	=		⇒ a=
sinβ		sin(α+β)		sin(α+β)

	b		d		dsin(2α+β)
i		=		⇒ b=
	sin(2α+β)		sin(α+β)		sin(α+β)