twierdzenie sinusów i cosinusów
salamandra:
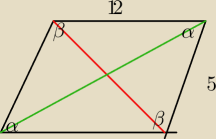
W równoległoboku ABCD boki mają długości 12 i 5, a krótsza przekątna ma długość 8. Oblicz
długość drugiej przekątnej.
2
Czy to jest dobry rysunek? Jest różnica którą przekątną uznam za krótszą?
16 sty 21:05
Blee:
żadna różnica ... o ile rysunek nie będzie sugerował innej

16 sty 21:10
salamandra: Mając trzy boki trójkąta 12,5,8, najlepiej z tw. cosinusów i wyliczyć ile będzie wynosił cosα?
16 sty 21:11
Blee:
dokładnie
16 sty 21:14
Blee:
i pamiętać, że α ≤ 90
o 
16 sty 21:15
salamandra: Bo nie leży naprzeciwko największego boku, więc nie mogą być dwa kąty rozwartokątne w
trójkącie?
16 sty 21:17
Blee:
yeeeep ... tylko 'największy bok' zamieniłbym na 'dłuższą przekątną'

i to że α+β = 180
16 sty 21:19
salamandra: tylko z tego, że α+β = 180 nie wynika wprawdzie, że α (ogółem) nie może być rozwarty?
16 sty 21:20
jc:
2(a2+b2)=p2+q2
a, b − boki
p, q − przekątne
16 sty 21:21
Blee:
powyższa zależność wynika z tw. cosinusów + tego, że α+β=180 więc cosβ = −cosα
16 sty 21:24
salamandra:
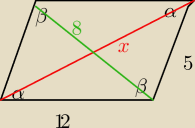
Wyliczyłem cosα
8
2=12
2+5
2 − 2*12*5*cosα
64=144+25−24*5*cosα
64= 171−120*cosα
−107 = 120cosα
α≈63
β = 180−63 = 117
I teraz tw.cos
x
2=12
2+5
2−2*12*5*cos117
x
2=144+25−120*(−cos63)
x
2=171−120*(−0,4540)
x
2=171−(−54,48)
x
2=225,48
x=
√225
Dobrze?
16 sty 21:29
salamandra: W odpowiedzi mam √274 i wynika to z rozbieżności w zaokrągleniach czy z jakiegoś błędu
elementarnego?
16 sty 21:29
salamandra: Nieważne, nie będzie 171 tylko 169.
16 sty 21:31
ABC: 144+25=169 to po pierwsze
po drugie gdy cosα wychodzi ujemny to druga ćwiartka
dalej mi się nie chce patrzeć

16 sty 21:33
salamandra: Faktycznie, nie wiem dlaczego zgubiłem minus przy 120cosα.
16 sty 21:34
salamandra: | | −105 | |
Znaczy tu zgubiłem, ale wynik i tak jest dobry, bo po prostu będzie |
| więc wyjdzie |
| | −120 | |
cos dodatni.
No a w tym "x
2...." to zamieniłem cos117 na −cos63
16 sty 21:35
a@b:
Skorzystaj z zależności ( już Ci ją podawałam
f2+e2=2a2+2b2
f
2=2*144+2*25 −64
f=
√274
========
i po ptokach

16 sty 21:36
ABC:
robisz to od zakrystii, ze wzorów redukcyjnych wyszedłby dokładny wynik √105+169= √274
książka ma dobrze
16 sty 21:37
salamandra: a@b tak, tylko temat mam zastosowania tw. sinusów i cosinusów, więc musiałbym pewnie dowieść
tego wzoru, a nie znam dowodu tego wzoru.
Po poprawce tych chochlików i tak wychodzi mi √227.... więc coś mam źle
16 sty 21:38
ABC:
Eta ty już wybiłaś tyle ptaków a do mnie wrony przylatują cały czas

16 sty 21:39
Saizou :
Dowód wynika z automatu z tw. cosinusów

16 sty 21:39
ABC:
salamandra bo tam nie wychodzi za Chiny Ludowe kąt 63 jaki ty podajesz
16 sty 21:40
a@b:
Dowód prosty ....jak "budowa cepa"

e
2=a
2+b
2−2abcosα β=180
o−α to cosβ= −cosα
zatem f
2=a
2+b
2−
+2abcosα
dodając stronami otrzymasz
f2+e2=2a2+2b2
i po b
ólu

16 sty 21:42
salamandra: Napiszę rozwiązanie od nowa:
8
2=12
2+5%2−2*12*5*cosα
64=144+25−120cosα
64=169−120cosα
−105=−120cosα
cosα=0,875
α≈61
β=119
x
2=12
2+5%2−2*12*5*cos119
x
2=169−120*(−cos61)
x
2=169−120*(−0,4848)
x
2=169+58,176≈227
x=
√227
Coś zrobiłem źle?
16 sty 21:42
jc: A ja myślałem, że to tożsamość równoległoboku:
(u+v)2 + (u−v)2 = 2(u2+v2)
u=C−A, v=D−B
16 sty 21:43
ABC:
cos α=0,875 to α≈28 stopni 57 minut 18 sekund
16 sty 21:43
a@b:
@
ABC
Kup sobie "sztuczną wronę" u Chińczyka i zamontuj..( to żywe wrony odstraszysz

16 sty 21:45
salamandra: Ohhh jezuuu, nie pierwszy raz źle przeczytałem z tablic, bo przeczytałem dla kąta α, a dla cos
trzeba odczytywać z β

16 sty 21:45
a@b:
@
jc jasne ,że
tożsamość
Jak zwał, tak zwał

16 sty 21:46
salamandra: Teraz wyszło, dzięki

16 sty 21:51
salamandra: a@b− f2=a2+b2−+2abcosα− to w końcu − czy + tu będzie (mówię o tym dowodzie)
16 sty 21:52
a@b:
plus
16 sty 21:53
salamandra: bo formalnie powinno być 2abcosβ ale już zamieniłaś na α i minusy pomnożyłaś tak?
16 sty 21:54
a@b:
taaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaak

16 sty 21:54
salamandra: Postaram się zapamiętać tę zależność

16 sty 21:55
a@b:

16 sty 21:55
salamandra: Przydała się już w następnym zadaniu:
W równoległoboku przekątnę mają długości 10 i 6
√2. Oblicz sumę kwadratów długości dwóch
różnych boków tego równoległoboku.
10
2+(6
√2)
2=2a
2+2b
2
100+36*2=2a
2+2b
2
172=2a
2+2b
2/ :2
86=a
2+b
2
dziękuję

16 sty 21:58
a@b:

Pamiętaj!
Musisz na początku dopisać komentarz
w każdym równoległoboku zachodzi równość
f2+e2=2a2+2b2
16 sty 22:04
salamandra:
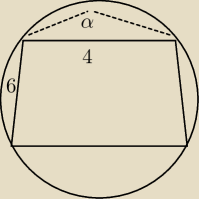
Teraz mam problem z następującym zadaniem, nie wiem czy dobrze do niego podchodzę−
Trapez równoramienny wpisany jest w okrąg o(O,R). Przedłużenia ramion trapezu przecinają się
pod kątem 60 stopni.
Oblicz promień R okręgu, jeśli ramię trapezu ma dlugość 6, a krótsza podstawa 4.
Oczywiście rysunek niedokładny, ale chodzi o to, że skoro przecinają się pod kątem 60 stopni,
to razem z trapezem powstaje mi trójkąt równoboczny i z tego trzeba kombinować?
16 sty 22:06
a@b:
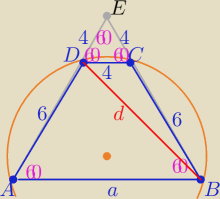
1/ z podobieństwa trójkątów ABE i DCE
.............
a=10
Z tw cosinusów w ΔABD
d
2=.....................
i z tw. sinusów w tym samym trójkącie
R=...........
16 sty 22:25
a@b:
Myślę,że to wiesz : ΔABE jest równoboczny
16 sty 22:32
salamandra:
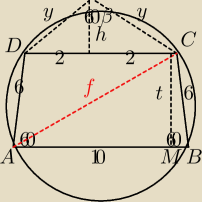
Zrobiłem to trochę inaczej:
Z małego trójkąta powstałego wskutek przedłużenia ramion:
h
√3 = 6
3h= 6
√3
h=2
√3
y
√3 = 4
√3
3y=12
y=4
Wiemy, że powstanie nam trójkąt równoboczny, więc skoro y=4, to całe ramię ma 6+4 = 10, więc
dolna podstawa również ma 10.
Teraz rozważam trójkąt MBC
| | a−b | | 10−4 | |
Z własności trapezu wiem, że |MB| to |
| = |
| =3 |
| | 2 | | 2 | |
Z tw. Pitagorasa liczę wysokość trójkąta MBC oznaczoną t.
t
2+3
2=36
t
2=27
t=
√27
Teraz rozważam trójkąt AMC, liczę długość f
| | a+b | |
Wiem, że długość AM = |
| = 7 |
| | 2 | |
7
2+t
2 = m
2
49+27 = m
2
m=
√76
Z tw. sinusów w trójkącie ABC
| | √76*√3 | | √228 | | 2√57 | |
R= |
| = |
| = |
| |
| | 3 | | 3 | | 3 | |
16 sty 22:44
Blee:
salamandra ... a nawet jeżeli nie zapamiętasz to ją wyprowadzisz z tw. cosinusów:
e2 = a2 + b2 − 2abcosα
f2 = a2 + b2 − 2abcosβ = a2 + b2 − 2abcos(180−α) = a2 + b2 +2abcosα
sumujemy i mamy:
e2 + f2 = 2a2 + 2b2
16 sty 22:45
salamandra: Tam nie m2 tylko f2, po prostu w zeszycie podpisałem to jako m i przepisywałem.
16 sty 22:46
a@b:
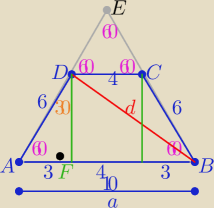 2 sposób
2 sposób ( bez podobieństwa
Kąty ostre trapezu mają po 60
o ( bo ΔABE równoboczny
Z trójkąta AFD "ekierki"
|AF|= 3 ... to a=10
Okrąg opisany na trapezie jest też opisany na ΔABD
z tw. cosinusów d=...........
zatem z tw. sinusów
R=..............
16 sty 22:48
a@b:
@
salamandra
Co to za rysunek ?

Zapamiętaj ! w zadaniach z planimetrii
porządny rysunek, to połowa sukcesu
16 sty 22:51
salamandra: Już mówiłem nie raz, że nie umiem tu rysować.
16 sty 22:52
a@b:
No ja teraz idę na
brydża
Powodzenia w następnych zadankach
16 sty 22:58
Szkolniak:
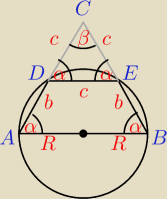
b=6
c=4
β=60
o
w ΔABC: α+α+β=180
o ⇔ 2α=120
o ⇔ a=60
o
|CD|=|CE|=|DE|=4
ΔABC~ΔDEC (cecha kkk)
2R=10 ⇒ R=5
Jeśli R wychodzi nieprawidłowe, w takim razie gdzie w moim rozumowaniu jest błąd?
16 sty 23:02
salamandra: A na pewno możesz założyć ze AB to 2R?
16 sty 23:07
Szkolniak: Ostatnio z
a@b rozwiązywaliśmy pewien dowód na pole takiego trapezu, wyszło bodajże
| | h2 | |
P= |
| , i wyszło na to że nie jest ważne jak narysuje ten trapez  |
| | tgα | |
Pytanie w takim razie w czym tkwi tutaj problem i czy mogę tak narysować tutaj ten trapez
16 sty 23:16
Bleee:
Szkopniak − dłuższą podstawa nie jest równa średnicy.
Zauważ że przy takim układzie prowadzisz bok że środka okręgu do wierzchołka C. Otrzymujesz
trójkąt rownoramienny (ramiona rowne R) którego kat przy podstawie równy jest 60o, w takim
razie to jest trójkąt rownoboczny, więc R = 6 (ramię trapezu)
Analogicznie do wierzchołka D i masz trójkąt ΔOCD który także będzie rownoboczny (patrz
kąty) więc krótsza podstawa by musiała się równać 6, a tyle się nie równa.
16 sty 23:32
Bleee:
Ale właśnie pdsunales mi pomysł na rozwiazanie. Zaraz będę rysować.
16 sty 23:35
Szkolniak: Bleee rzeczywiście, dzięki

17 sty 00:33
a@b:

17 sty 00:35
 W równoległoboku ABCD boki mają długości 12 i 5, a krótsza przekątna ma długość 8. Oblicz
długość drugiej przekątnej.
2
Czy to jest dobry rysunek? Jest różnica którą przekątną uznam za krótszą?
W równoległoboku ABCD boki mają długości 12 i 5, a krótsza przekątna ma długość 8. Oblicz
długość drugiej przekątnej.
2
Czy to jest dobry rysunek? Jest różnica którą przekątną uznam za krótszą?


 i to że α+β = 180
i to że α+β = 180
 Wyliczyłem cosα
82=122+52 − 2*12*5*cosα
64=144+25−24*5*cosα
64= 171−120*cosα
−107 = 120cosα
α≈63
β = 180−63 = 117
I teraz tw.cos
x2=122+52−2*12*5*cos117
x2=144+25−120*(−cos63)
x2=171−120*(−0,4540)
x2=171−(−54,48)
x2=225,48
x= √225
Dobrze?
Wyliczyłem cosα
82=122+52 − 2*12*5*cosα
64=144+25−24*5*cosα
64= 171−120*cosα
−107 = 120cosα
α≈63
β = 180−63 = 117
I teraz tw.cos
x2=122+52−2*12*5*cos117
x2=144+25−120*(−cos63)
x2=171−120*(−0,4540)
x2=171−(−54,48)
x2=225,48
x= √225
Dobrze?




 e2=a2+b2−2abcosα β=180o−α to cosβ= −cosα
zatem f2=a2+b2−+2abcosα
dodając stronami otrzymasz
f2+e2=2a2+2b2
i po bólu
e2=a2+b2−2abcosα β=180o−α to cosβ= −cosα
zatem f2=a2+b2−+2abcosα
dodając stronami otrzymasz
f2+e2=2a2+2b2
i po bólu









 Pamiętaj!
Musisz na początku dopisać komentarz
w każdym równoległoboku zachodzi równość
f2+e2=2a2+2b2
Pamiętaj!
Musisz na początku dopisać komentarz
w każdym równoległoboku zachodzi równość
f2+e2=2a2+2b2
 Teraz mam problem z następującym zadaniem, nie wiem czy dobrze do niego podchodzę−
Trapez równoramienny wpisany jest w okrąg o(O,R). Przedłużenia ramion trapezu przecinają się
pod kątem 60 stopni.
Oblicz promień R okręgu, jeśli ramię trapezu ma dlugość 6, a krótsza podstawa 4.
Oczywiście rysunek niedokładny, ale chodzi o to, że skoro przecinają się pod kątem 60 stopni,
to razem z trapezem powstaje mi trójkąt równoboczny i z tego trzeba kombinować?
Teraz mam problem z następującym zadaniem, nie wiem czy dobrze do niego podchodzę−
Trapez równoramienny wpisany jest w okrąg o(O,R). Przedłużenia ramion trapezu przecinają się
pod kątem 60 stopni.
Oblicz promień R okręgu, jeśli ramię trapezu ma dlugość 6, a krótsza podstawa 4.
Oczywiście rysunek niedokładny, ale chodzi o to, że skoro przecinają się pod kątem 60 stopni,
to razem z trapezem powstaje mi trójkąt równoboczny i z tego trzeba kombinować?
 1/ z podobieństwa trójkątów ABE i DCE
.............
a=10
Z tw cosinusów w ΔABD
d2=.....................
i z tw. sinusów w tym samym trójkącie
1/ z podobieństwa trójkątów ABE i DCE
.............
a=10
Z tw cosinusów w ΔABD
d2=.....................
i z tw. sinusów w tym samym trójkącie
 Zrobiłem to trochę inaczej:
Z małego trójkąta powstałego wskutek przedłużenia ramion:
Zrobiłem to trochę inaczej:
Z małego trójkąta powstałego wskutek przedłużenia ramion:
 2 sposób ( bez podobieństwa
Kąty ostre trapezu mają po 60o ( bo ΔABE równoboczny
Z trójkąta AFD "ekierki"
|AF|= 3 ... to a=10
Okrąg opisany na trapezie jest też opisany na ΔABD
z tw. cosinusów d=...........
zatem z tw. sinusów
2 sposób ( bez podobieństwa
Kąty ostre trapezu mają po 60o ( bo ΔABE równoboczny
Z trójkąta AFD "ekierki"
|AF|= 3 ... to a=10
Okrąg opisany na trapezie jest też opisany na ΔABD
z tw. cosinusów d=...........
zatem z tw. sinusów
 Zapamiętaj ! w zadaniach z planimetrii
porządny rysunek, to połowa sukcesu
Zapamiętaj ! w zadaniach z planimetrii
porządny rysunek, to połowa sukcesu
 Powodzenia w następnych zadankach
Powodzenia w następnych zadankach
 b=6
c=4
β=60o
w ΔABC: α+α+β=180o ⇔ 2α=120o ⇔ a=60o
|CD|=|CE|=|DE|=4
ΔABC~ΔDEC (cecha kkk)
b=6
c=4
β=60o
w ΔABC: α+α+β=180o ⇔ 2α=120o ⇔ a=60o
|CD|=|CE|=|DE|=4
ΔABC~ΔDEC (cecha kkk)


