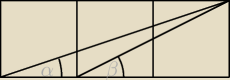
Maturalnie Saizou : Zadanka dla maturzystów − misz masz Zad 1 Na rysunku przestawiony jest prostokąt złożony z trzech przystających kwadratów. Uzasadnij, że α+β=45°. Zad 2

	a		c		4b
Uzasadnij, że jeśli a≠b, b≠c, c≠a i a+c=2b, to		+		=
	c−b		b−a		c−a

Zad 3 Oblicz pierwszy wyraz ciągu (x_n), n≥1, jeśli wiadomo, że a) wszystkie wyrazy ciągu (x_n) są dodatnie, b) ciąg (a_n) określony wzorem a_n=log₃(x_n), dla n≥1 jest ciągiem arytmetycznym c) x₃•x₅=48

Mariusz: Ad 1) Swego czasu miałem to zadanie na algebrze gdy chodziłem na zaoczne studia informatyczne Tam trzeba było je rozwiązać z użyciem mnożenia liczb zespolonych Może coś da się wykombinować z przejściem z kartezjańskiego układu współrzędnych na biegunowy

Saizou : Da się to rozwiązać korzystając tylko z geometrii, nie trzeba zespolonych ani współrzędnych biegunowych

Mariusz: Ja tylko napisałem że my na algebrze mieliśmy użyć liczb zespolonych

Wolfik: w drugim możemy wyliczyć a=2b−c, podstawić do lewej strony równania i przekształcać, aby była prawa strona?

Saizou : Napisałem to, żeby maturzystów nie odstraszyć

Saizou : Można, czyli chcesz zrobić coś takiego jak w tożsamościach trygonometrycznych

Wolfik: jest jeszcze inna metoda zrobienia tego? bo powychodziło mi coś takiego, że nie wiem czy ruszę dalej

Saizou : walcz ze swoją metodą, jest dobra

Wolfik: do tej pory:

a(b−a)+c(c−b)		2b2−2ab+cb+ac		2b(b−a)+c(b+a)
	=		=
(c−b)(b−a)		(c−b)(b−2b+c)		(c−b)2

Saizou : Ale mieszasz, skorzystaj dobrze z Twojego pomysłu, żeby wstawić a=2b−c w każde miejsce ze a po lewej stronie

Wolfik:

2b−c		c		2b
	+		=
c−b		b−2b+c		c−b

Saizou : Zobacz co musisz otrzymać (co musi być w mianowniku)

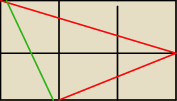
jc: Kolorowy trójkąt jest prostokątny i równoramienny. Kąt pomiędzy czerwonymi docinkami = 45^o.

Wolfik:

	2b
mogę z tej postaci co mam skorzystać?		? czy od nowa mam to rozpisywać, bo nie chce mi
	c−b

to wyjść

salamandra:

a		c		4b
	+		=
c−b		b−a		c−a

a+c = 2b a= 2b−c c= 2b−a

2b−c		c		4b
	+		=
c−b		b−(2b−c)		c−(2b−c)

2b−c		c		4b
	+		=
c−b		c−b		2c−2b

2(2b−c)		2c		4b
	+		=
2c−2b		2c−2b		2c−2b

4b−2c		2c		4b
	+		=
2c−2b		2c−2b		2c−2b

4b		4b
	=
2c−2b		2c−2b

Saizou : + komentarz salamandra Chociaż ładniej jest wyjść od lewej strony i dojść do prawej. @jc bardzo ładnie @Wolfik możesz od nowa, zobacz jak zrobił to @salamandra

salamandra: A nie wyszedłem od lewej?

Saizou : Przekształcasz dwie strony jednocześnie, nie jest to błąd.

salamandra: Po prostu po prawej zostawić w mianowniku (c−a) i potem lewą stronę zamienić na to?

salamandra: No i komentarz o przekształceniach równoważnych

Saizou :

a

c

2b−c

c

2b−c+c

2b

L=

+

=

+

=

=

=

c−b

b−a

c−b

b−(2b−c)

c−b

c−b

	2b		4b
=		=		=P
	a−c   c−   2		c−a

a@b: zad 1/ tgα= 1/3 , tgβ= 1/2

	tgα+tgβ
tg(α+β)=		=......
	1−tgα*tgβ

α+β=....

Tomek: W tym zadaniu 3 wyznaczyłbym wzór na x_n + x_n+1 i później odjął albo podzielił, nie wiem co by wyszło, albo ciąg geometryczny albo arytmetyczny, ale brakuje chyba w poleceniu wartości r=

Saizou :

	1
faktycznie,dla ciągu (an) różnica r=
	2

Szkolniak: Zadanie 3 a_n=log₃(x_n) ⇒ x_n=3^a_n, n≥1

	3an+1
(xn+1=3an+1 ∧ xn=3an) ⇒ q=		=3, zatem ciąg (xn) to ciąg
	3an

geometryczny, o ilorazie równym 3. x₃*x₅=x₁q²*x₁q⁴=x₁²q⁶=729x₁² x₃*x₅=48 729x₁²=48

	4		4√3
x1=		⇔ x1=
	9√3		27